modes complémentaires ( ‘réguliers’: MC )
séries générées par l’union de couleurs complémentaires
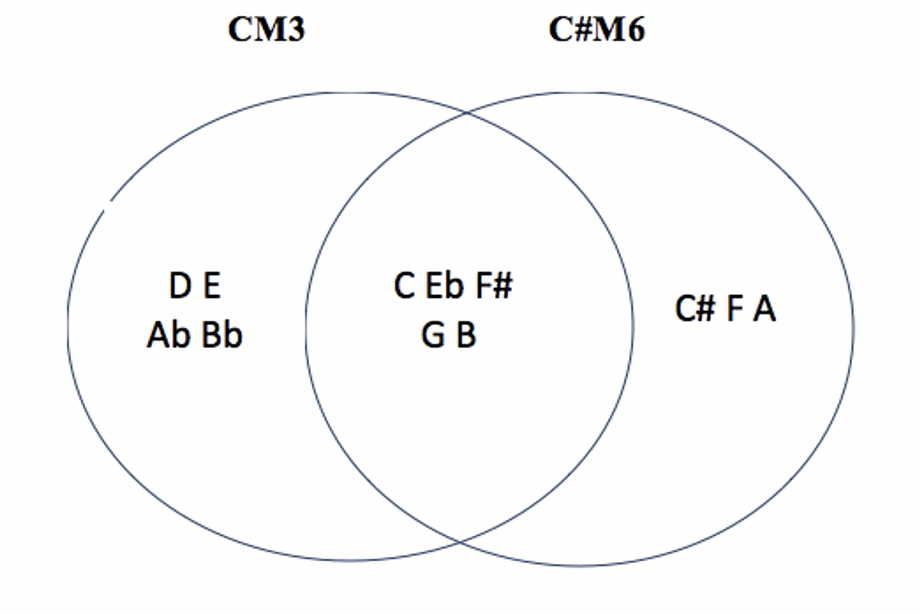
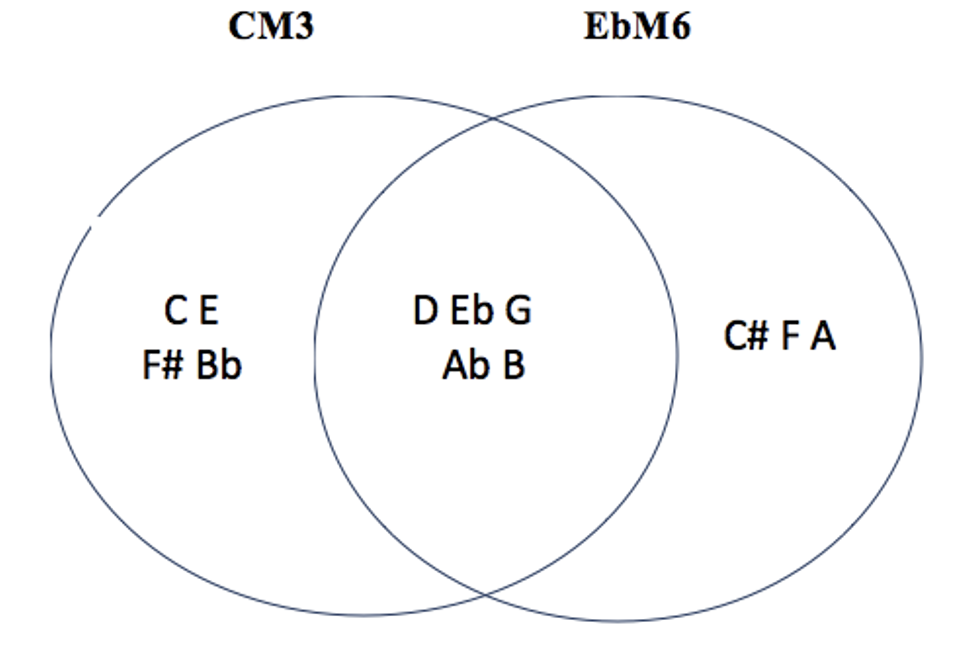
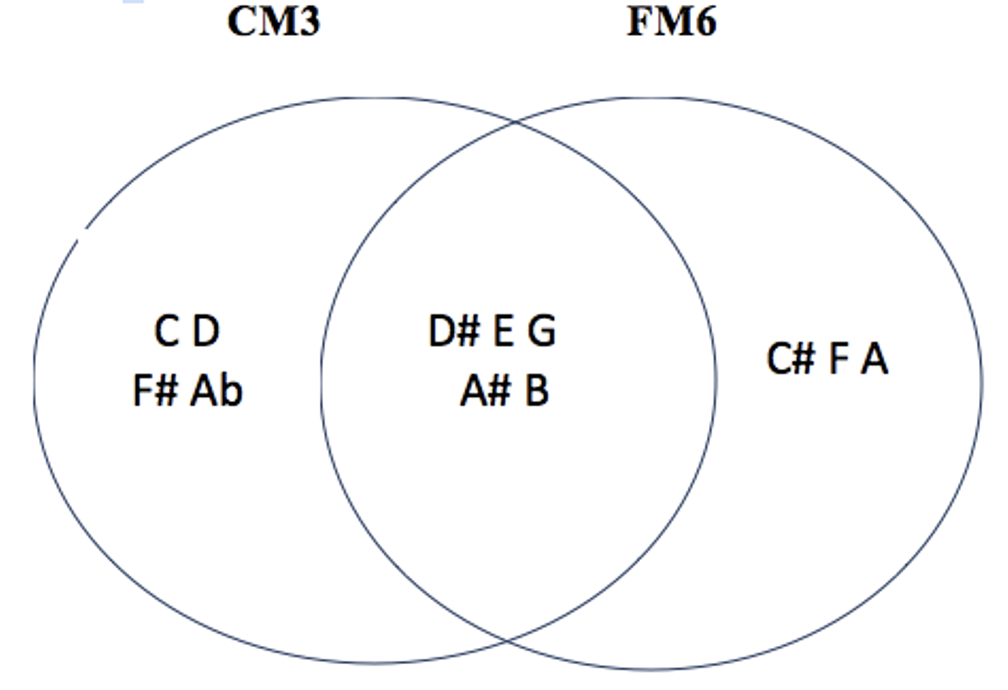
l’idée est de naviguer dans l’espace sériel en unissant des modes qu’on appelle ‘complémentaires : un groupe de 4 notes distinct pour chaque mode, et une portion commune de 4 notes : le total chromatique résonne par conséquence
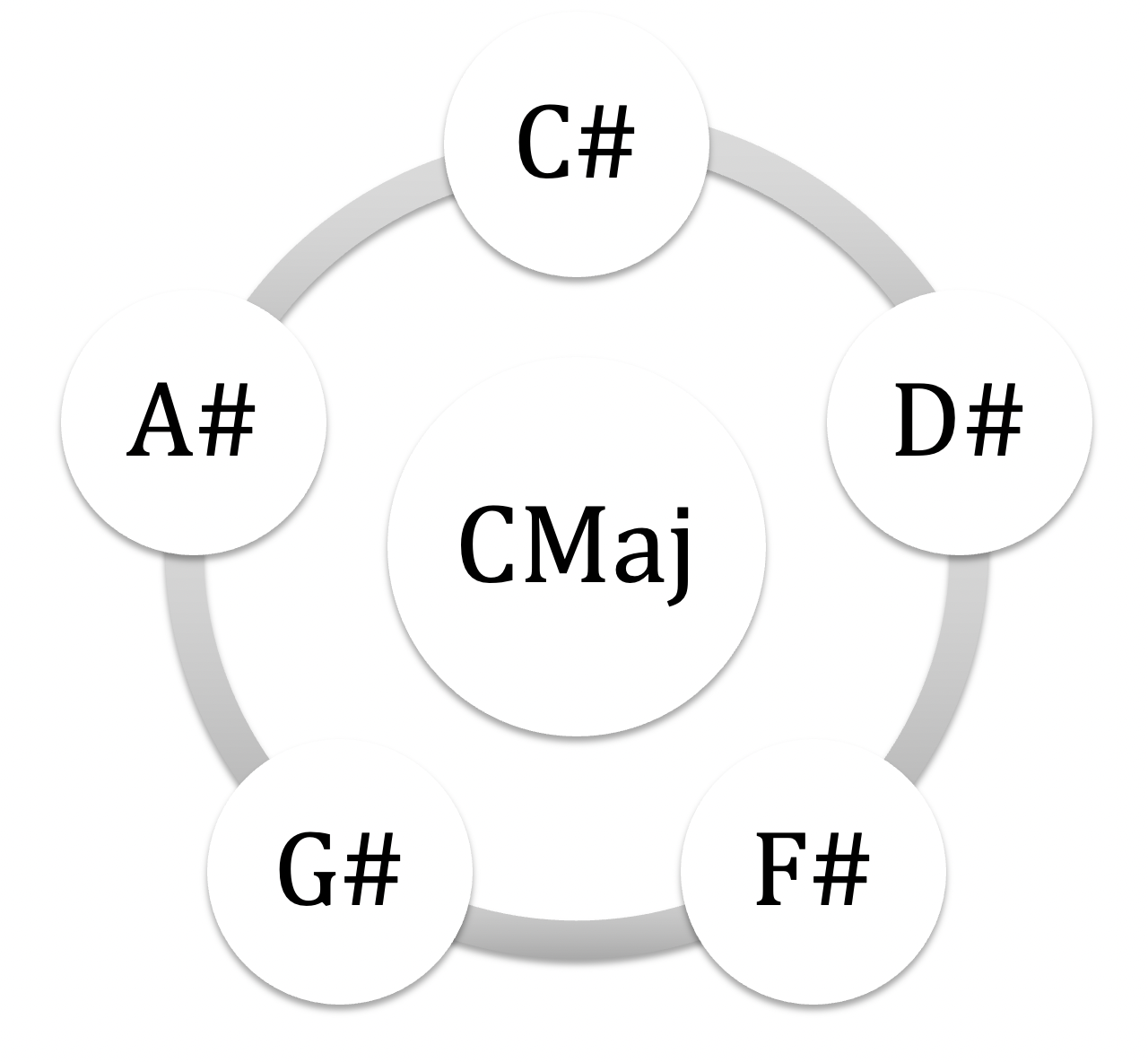
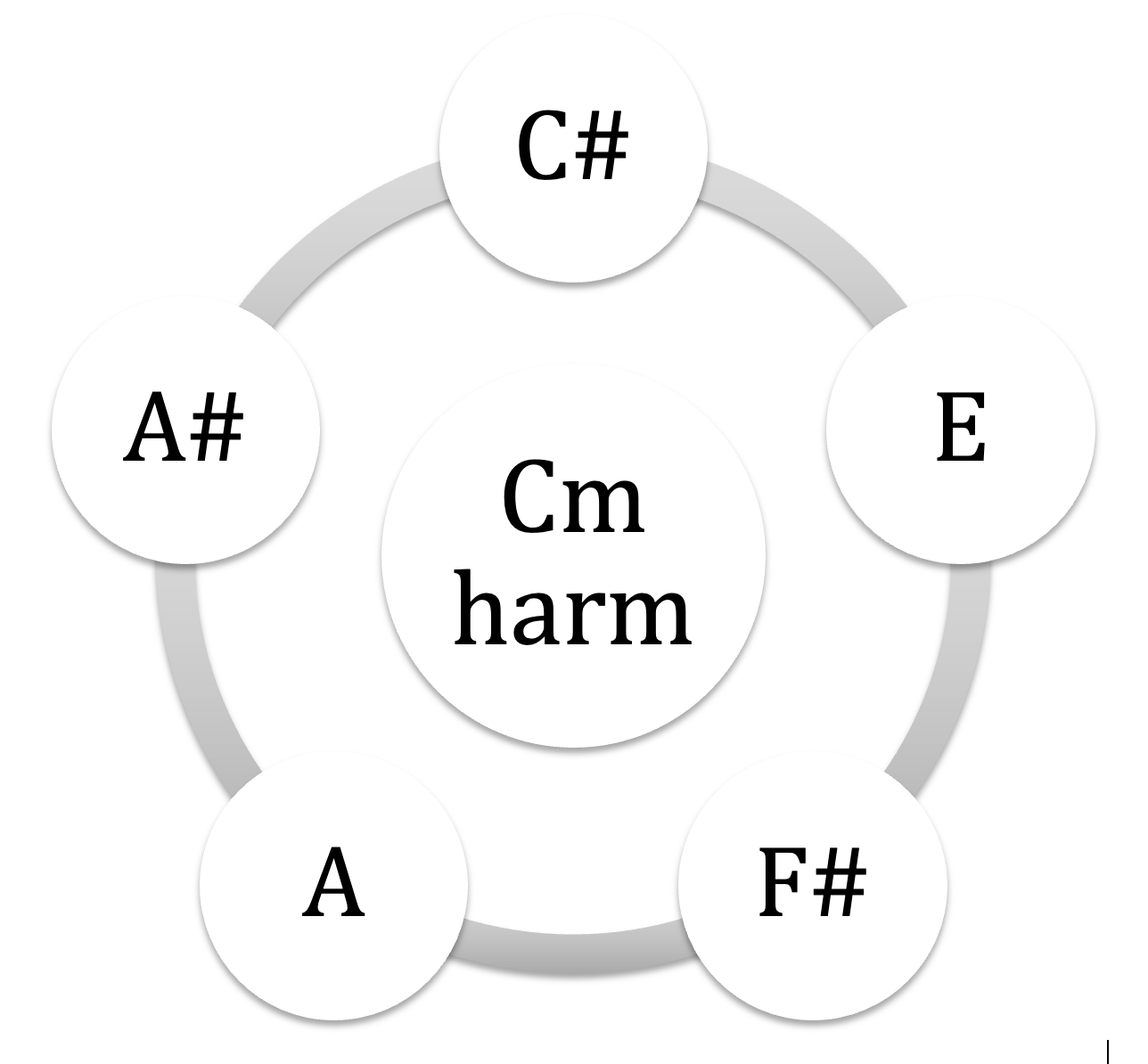
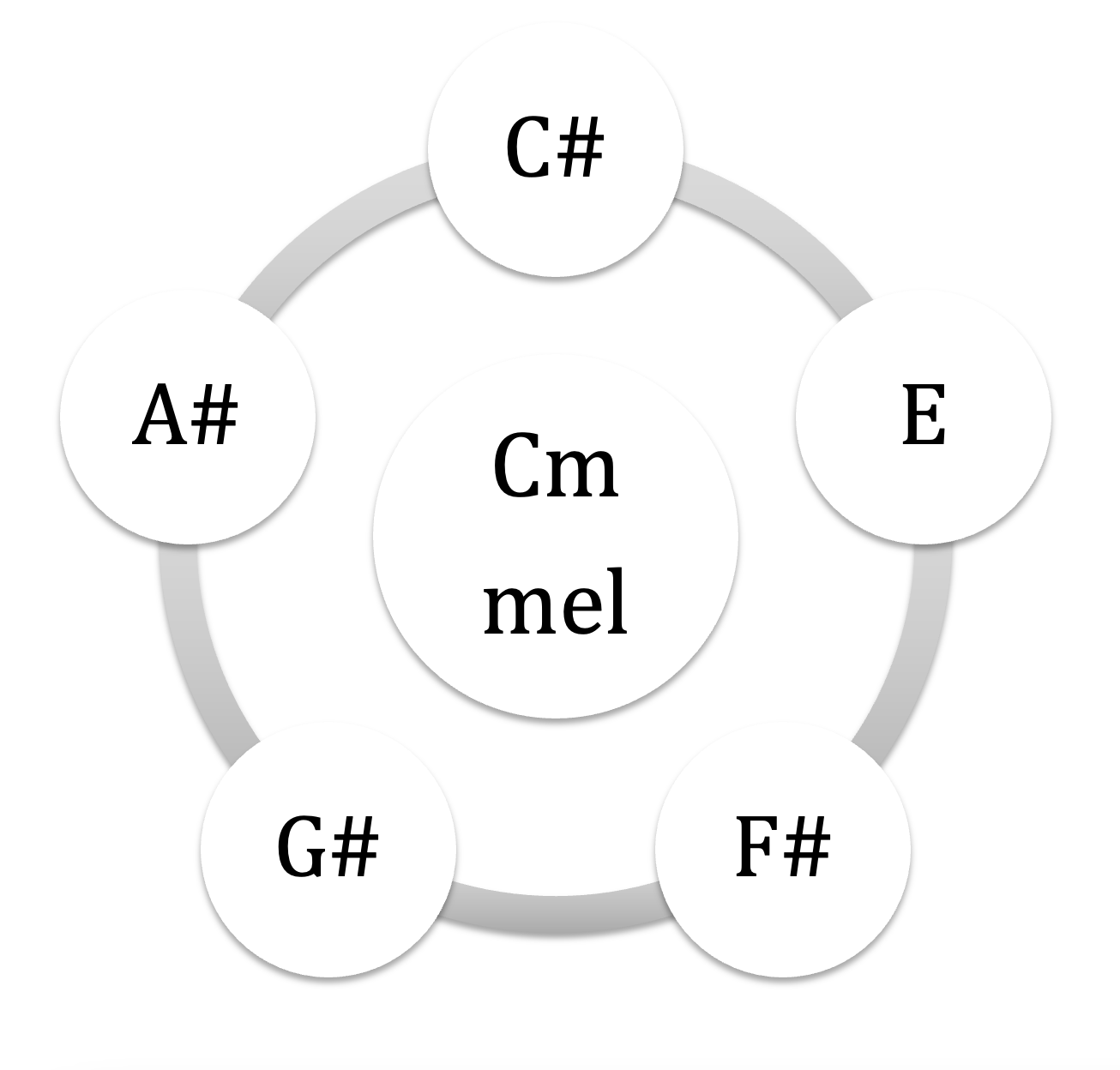
prenons les 3 pôles du système tonal majeur-mineur : majeur, mineur harmonique et mineur mélodique : visualisons ces 3 nucleus avec leurs compléments sériels: 3 séries pentatoniques aux couleurs référencées
Cmaj: CDEFGAB + F# maj pent
Cmin harm : CDEbFGAbB + F#7#9
Cmin mel : CDEbFGAB + F#9
par extension :
Cm dorien: CDEbFGABb + E maj pent
Cm phrygien : CDbEbFGAbBb + D maj pent
C lydien : CDEF#GAB + Db maj pent
C mixolydien : CDEFGABb + B maj pent
Cm aeolien : CDEbFGAbBb + A maj pent
Cm locrien : CDbEbFGbAbBb + G maj pent
appliquons le concept aux MATL :
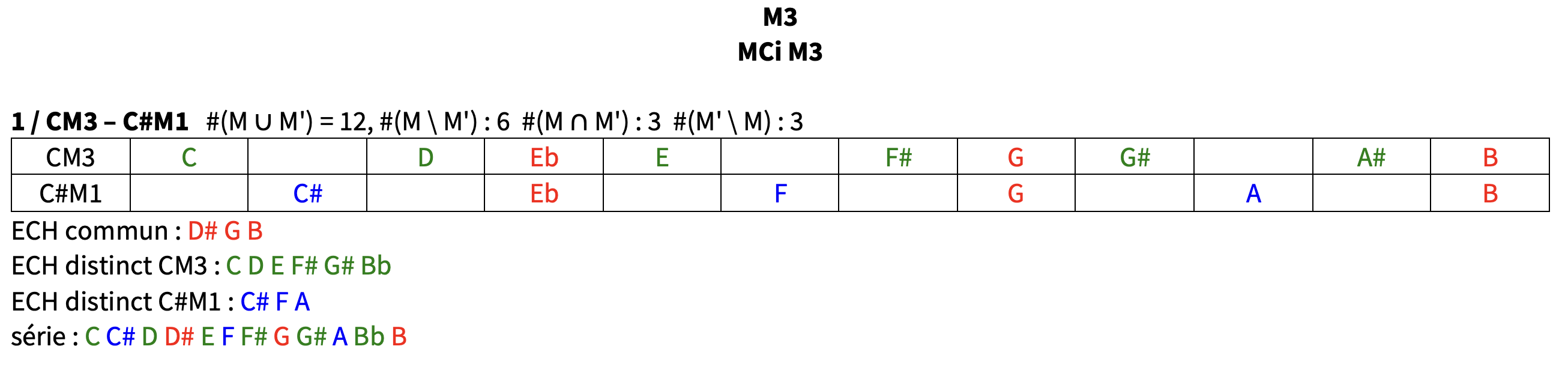
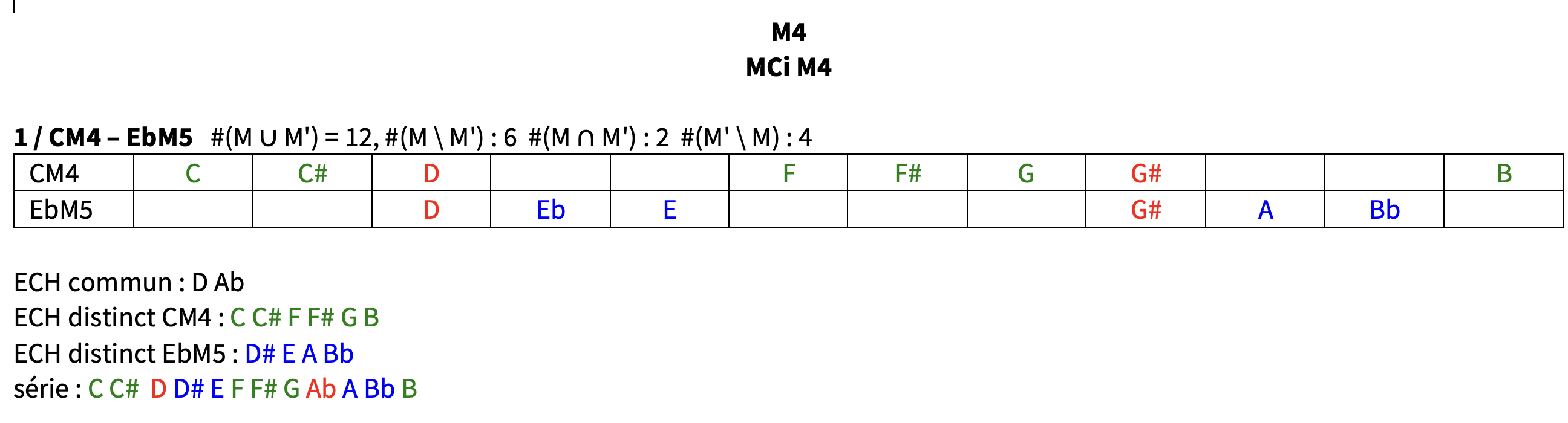
deux modes sont dits ‘complémentaires’ lorsque #(M ∪ M’) = 12, #(M \ M’) : 4 #(M ∩ M’) : 4 #(M’ \ M) : 4
( # représente le cardinal, ∪ représente l’union, \ représente la soustraction, ∩ représente l’intersection ) /
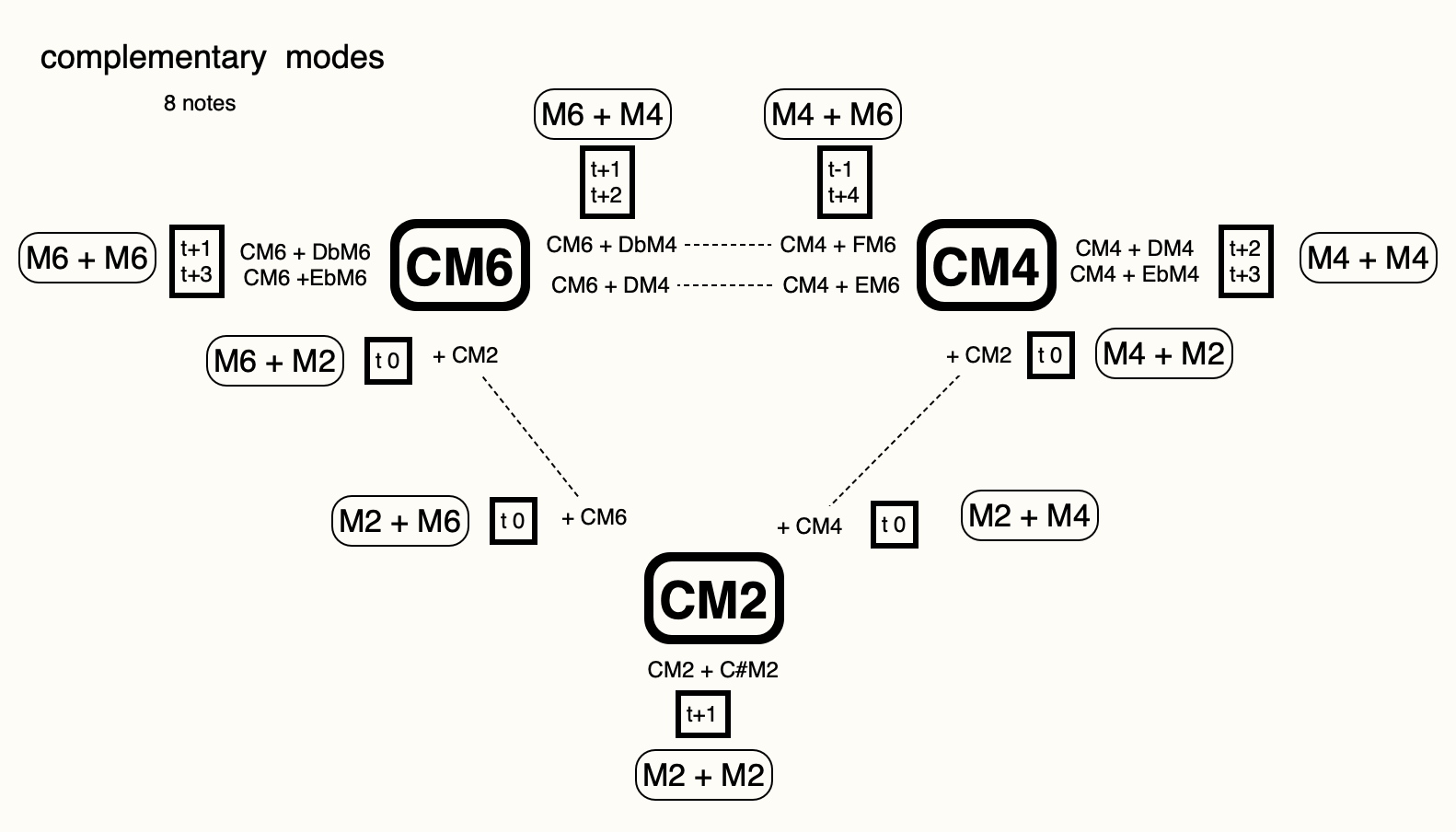
ainsi, un mode M’ est dit complémentaire à un mode donné M lorsqu’il peut être divisé en deux subsets de 4 notes: le premier subset est le complément dodécaphonique (CD) du mode donné M, et le deuxième subset est inclus dans le mode donné M/ l’union de leur PCset commun de 4 notes et de leurs deux PCset distincts ( 2 x 4 notes ) forme le total chromatique / chaque transposition de M2, M4 et M6 possède 6 modes complémentaires (MC)
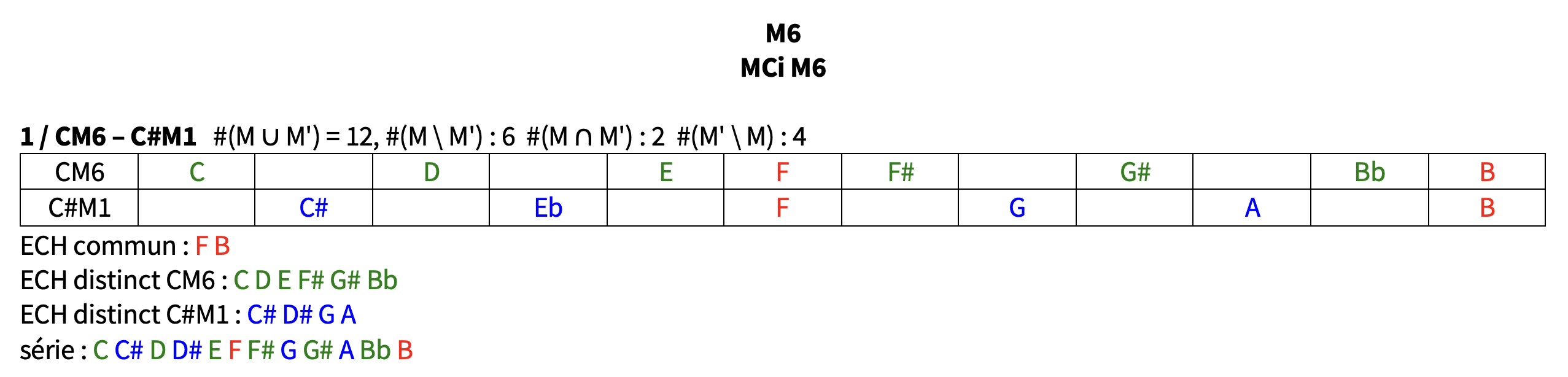
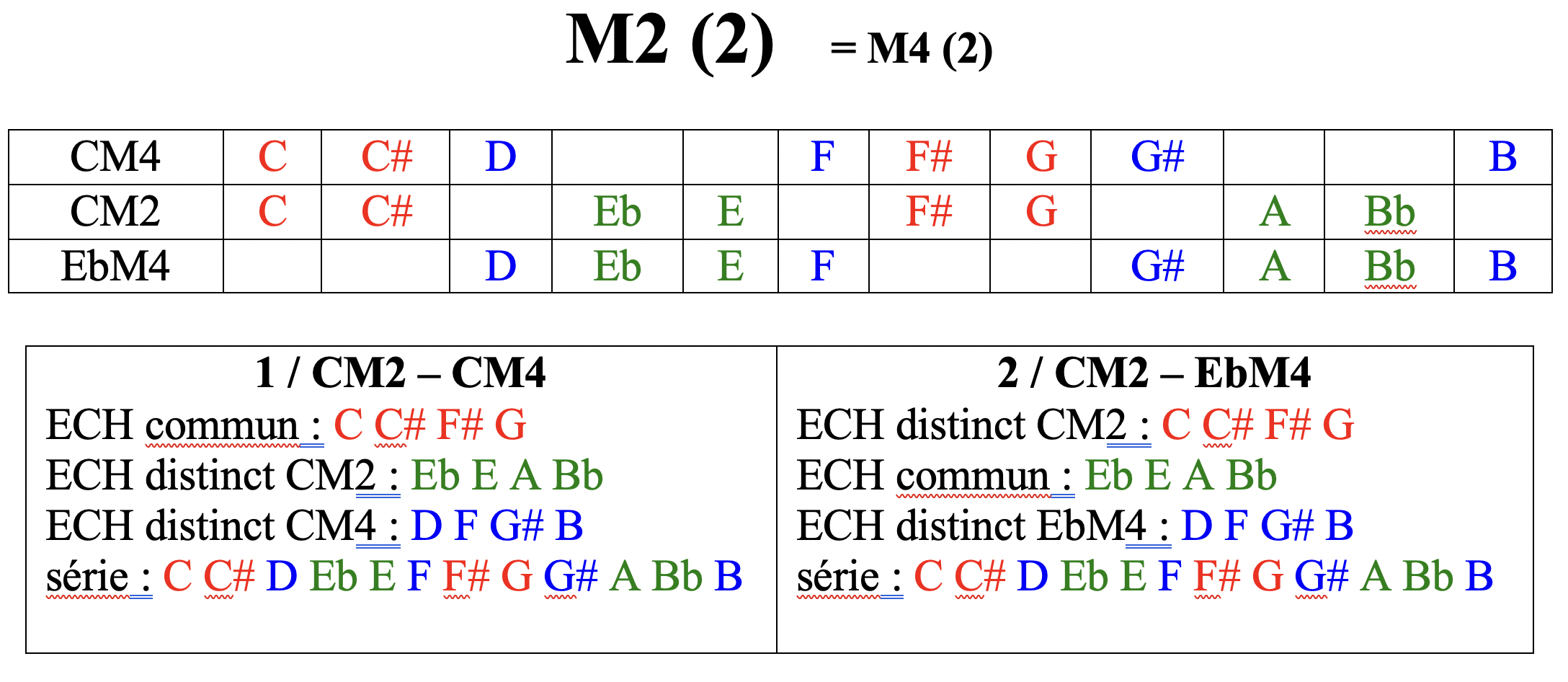
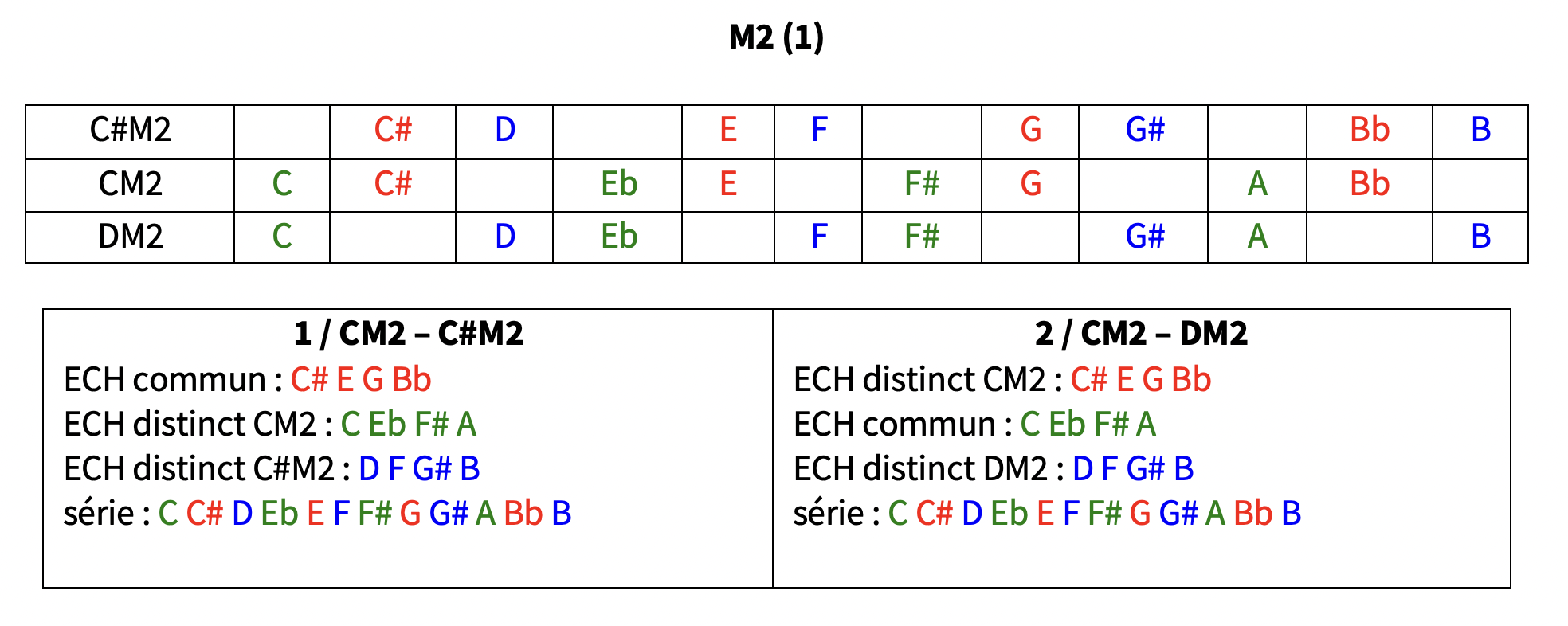
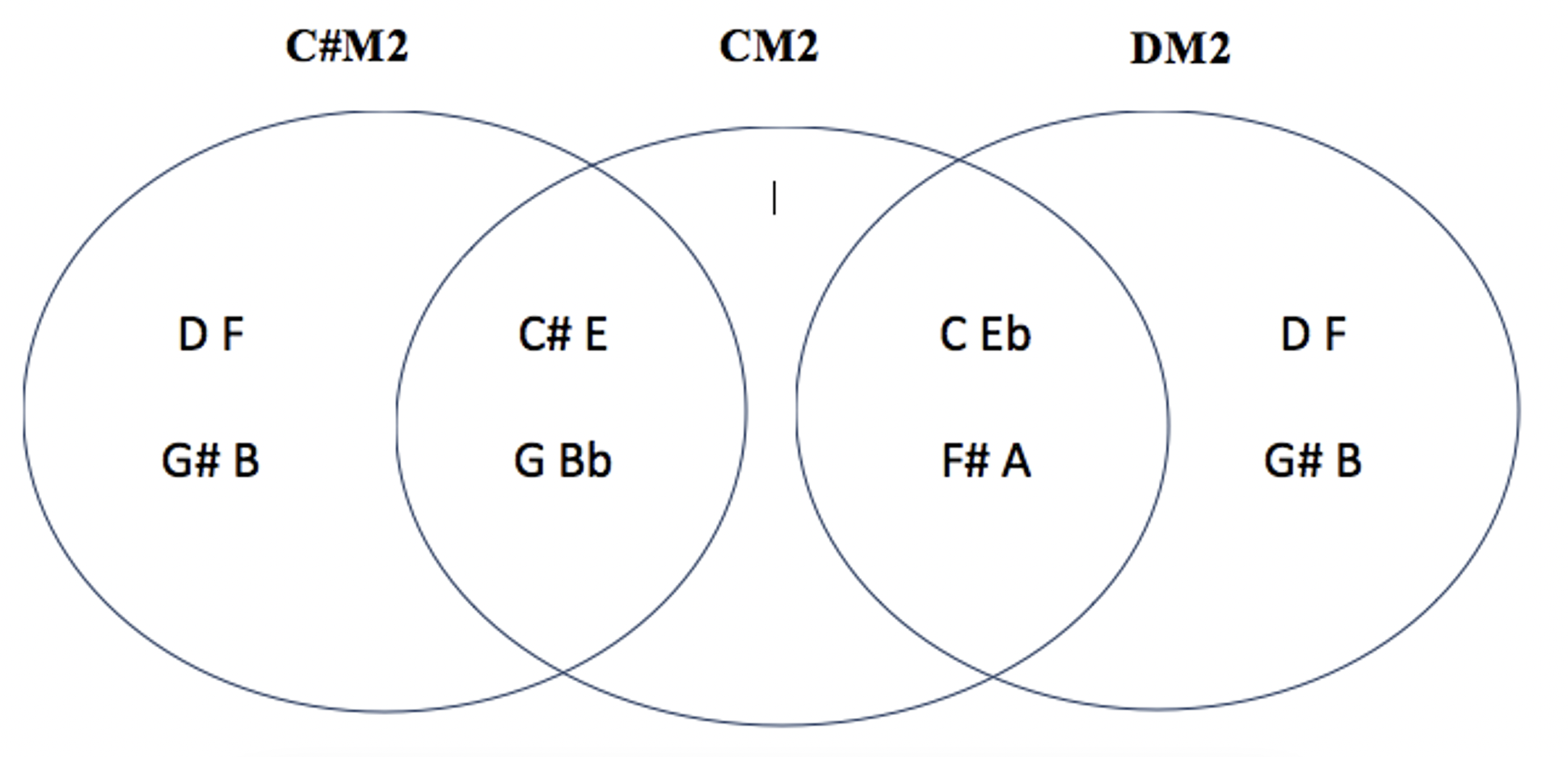
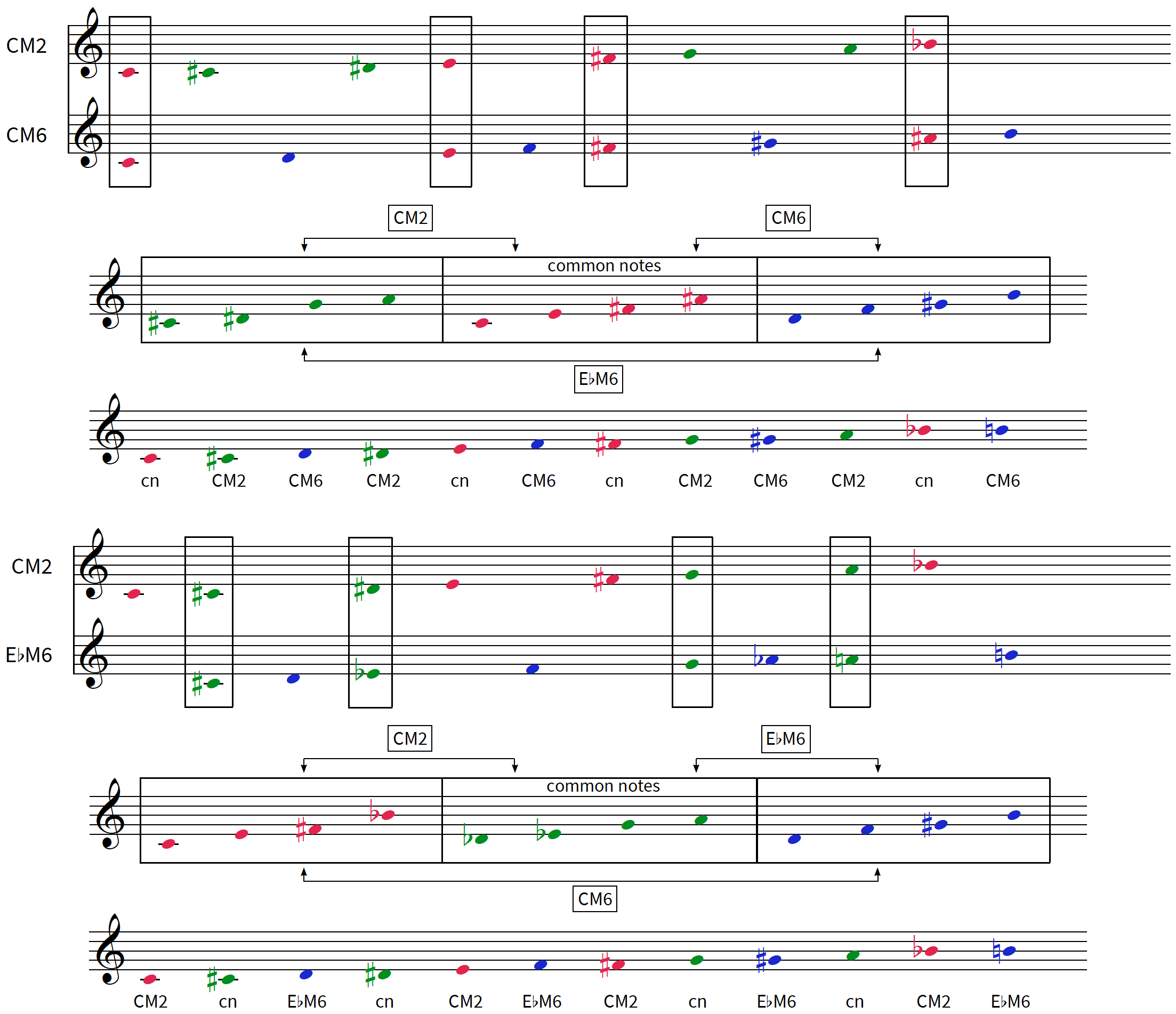
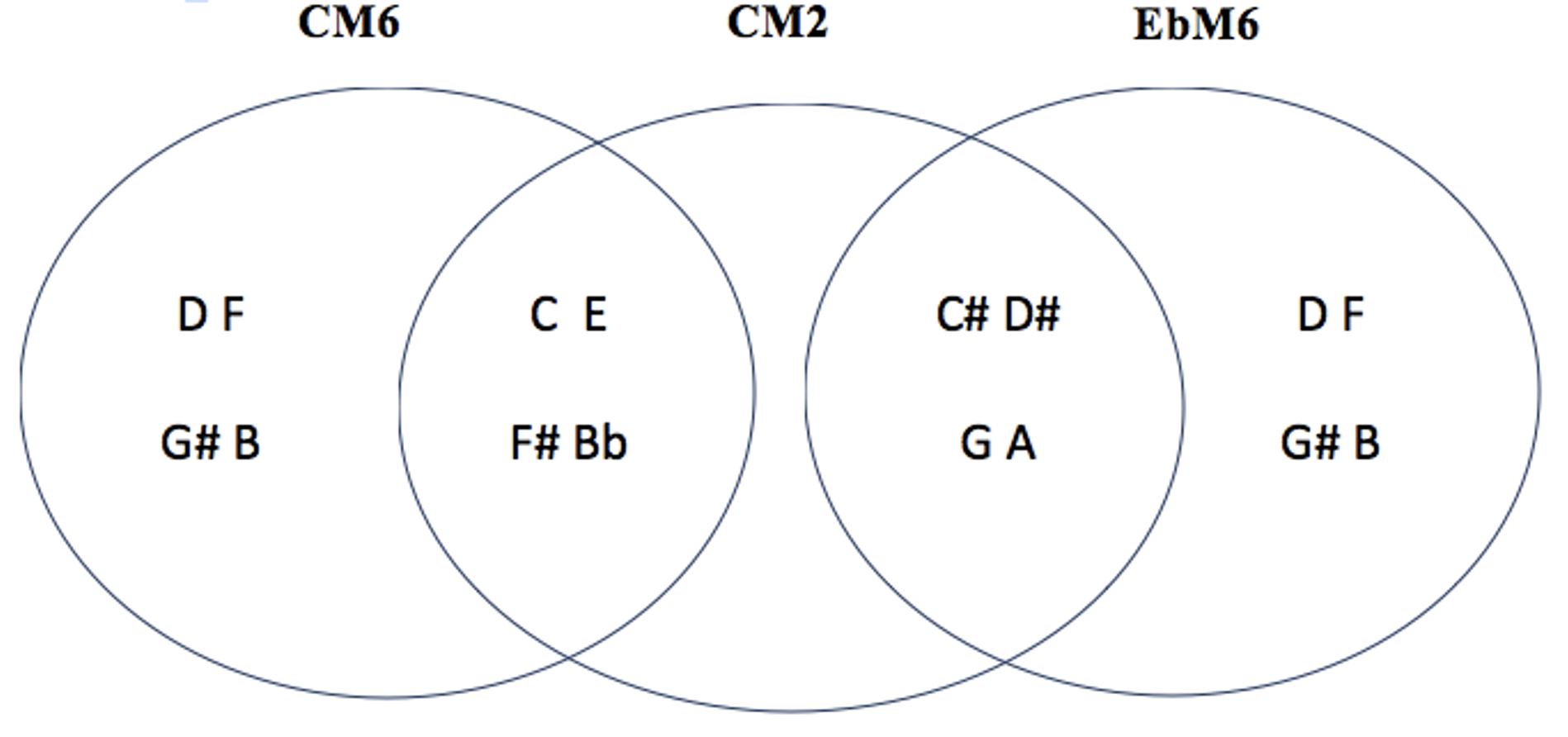
les 6 modes complémentaires de CM2 : C#M2 – DM2 / CM4 – EbM4 / CM6 – EbM6
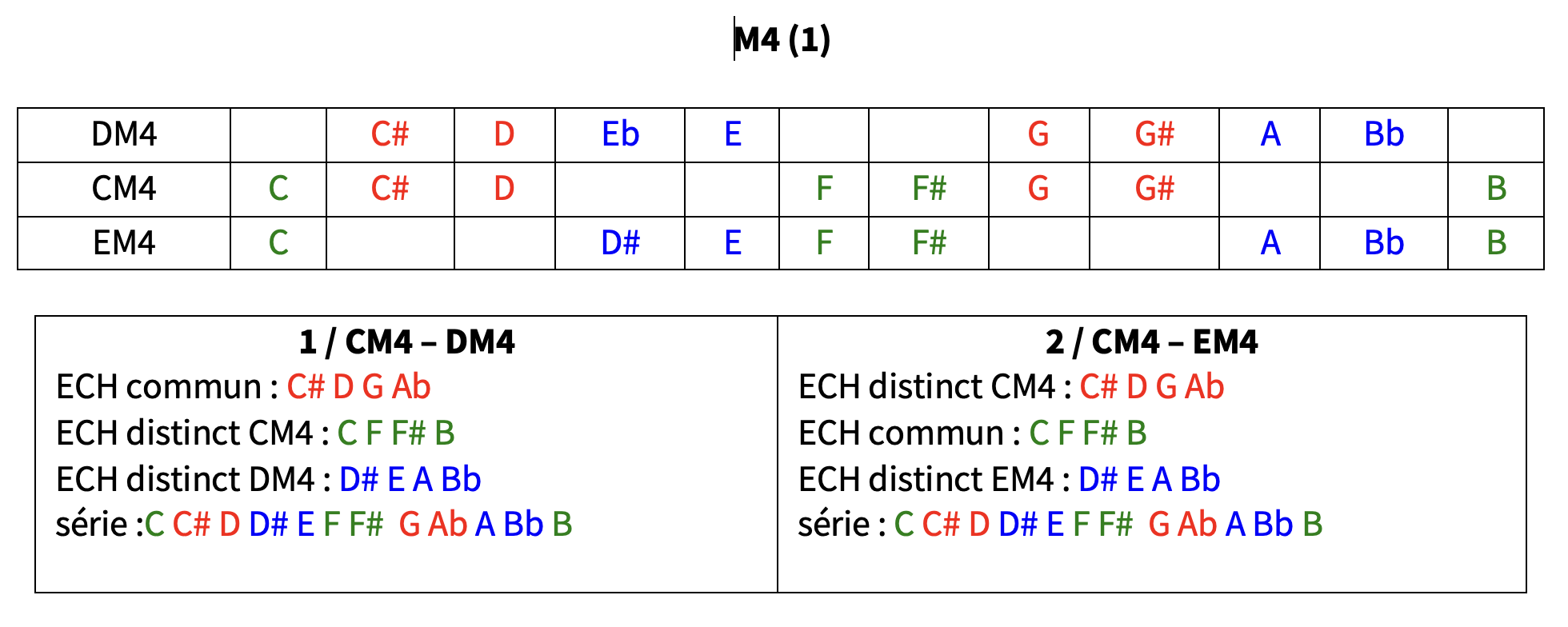
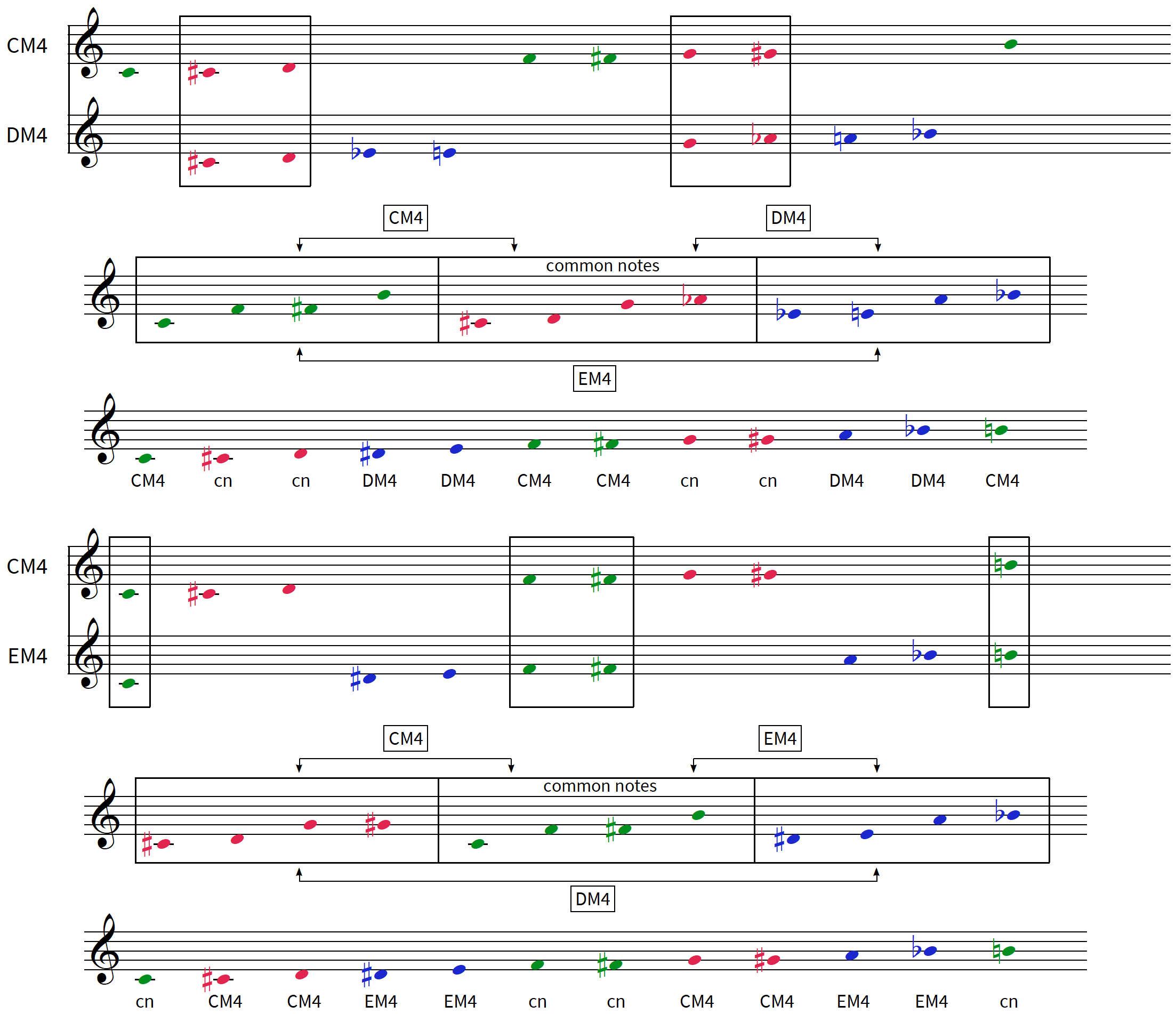
les 6 modes complémentaires de CM4 : DM4 – EbM4 / EM4 – CM2 / EM6 – FM6
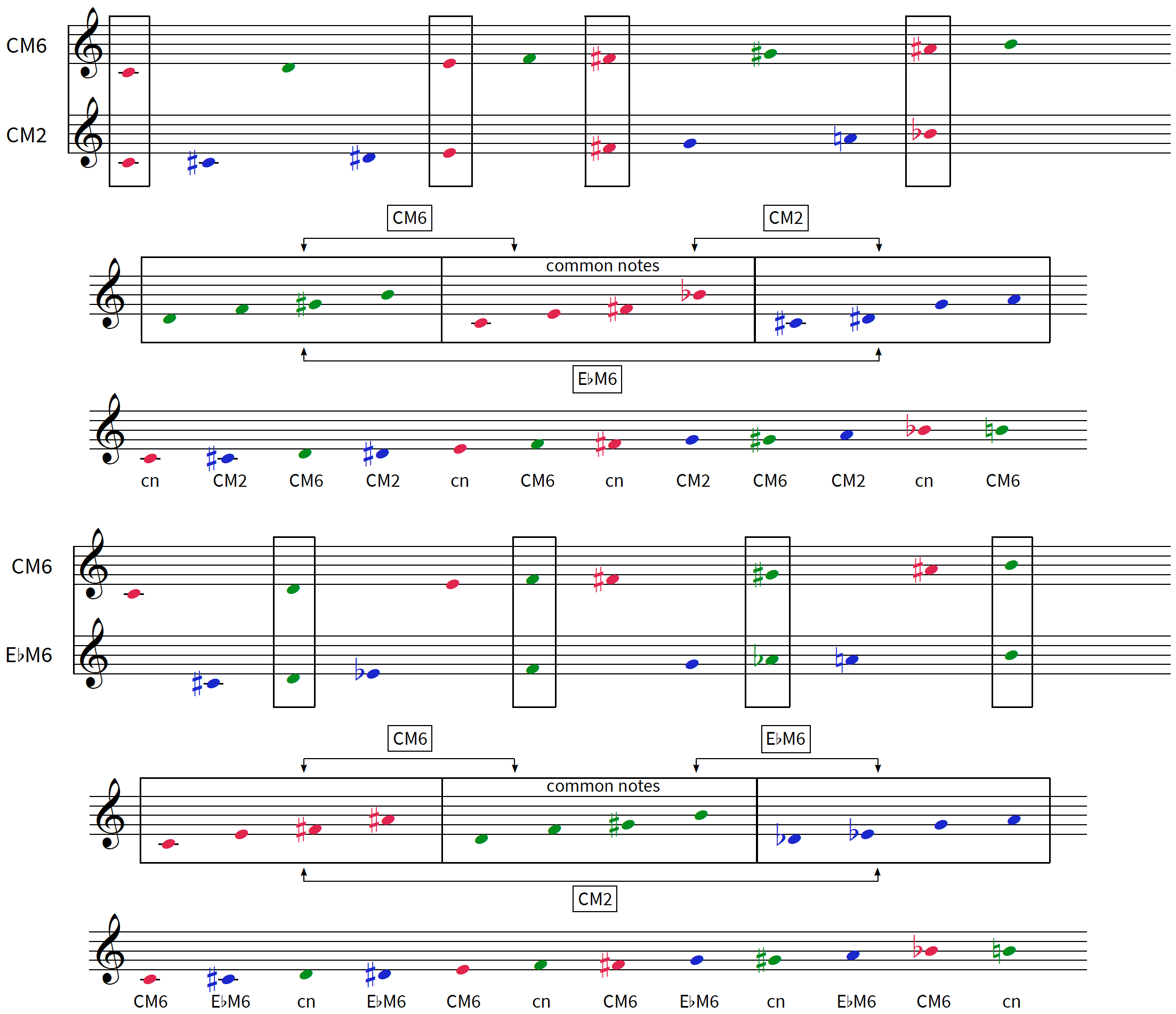
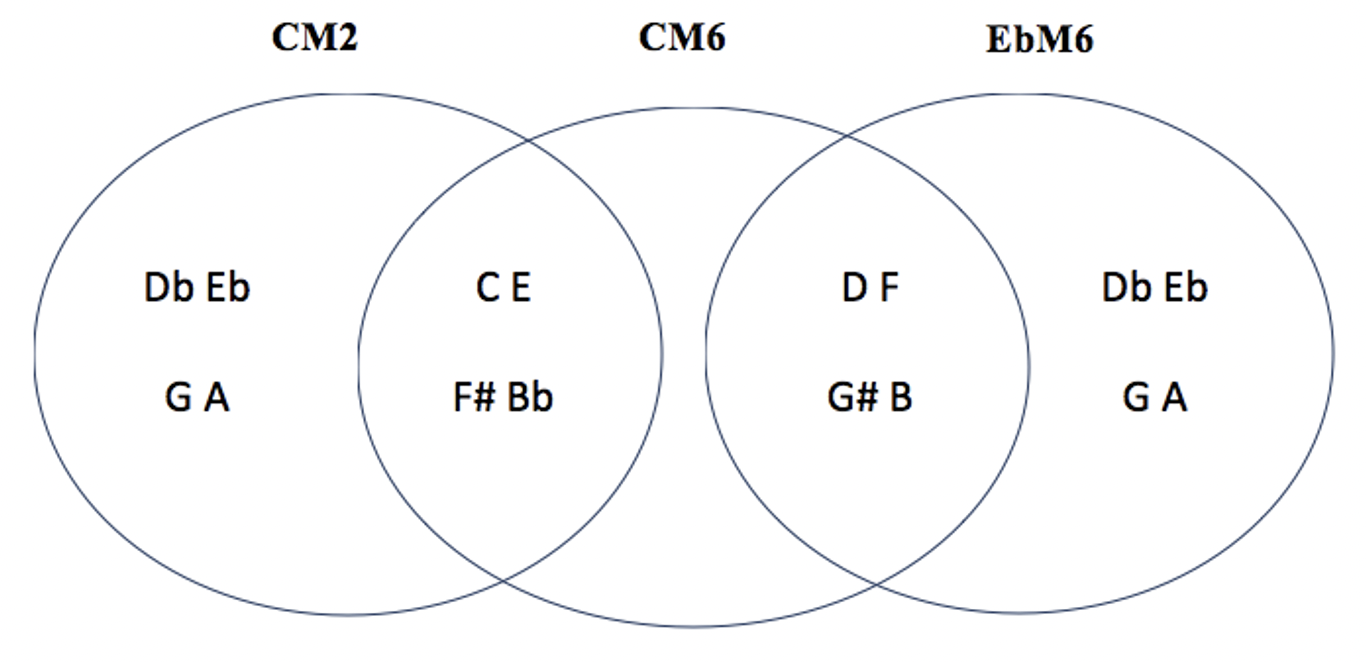
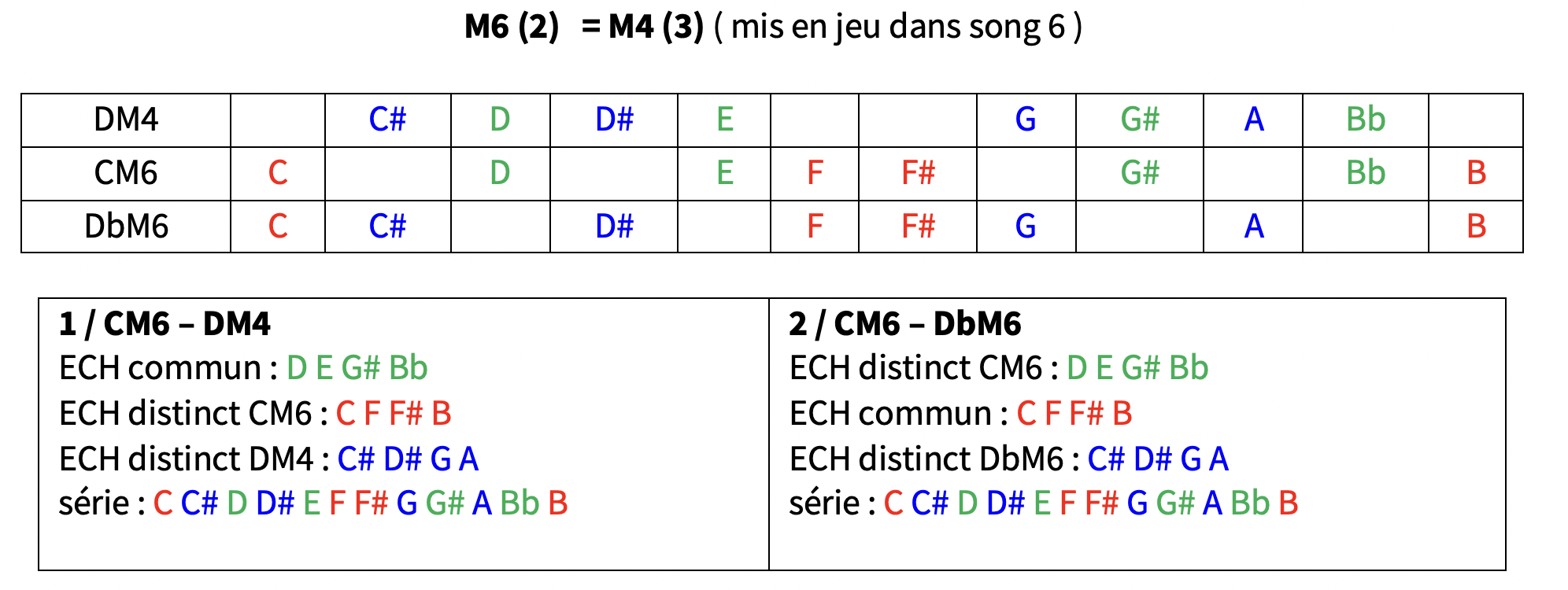
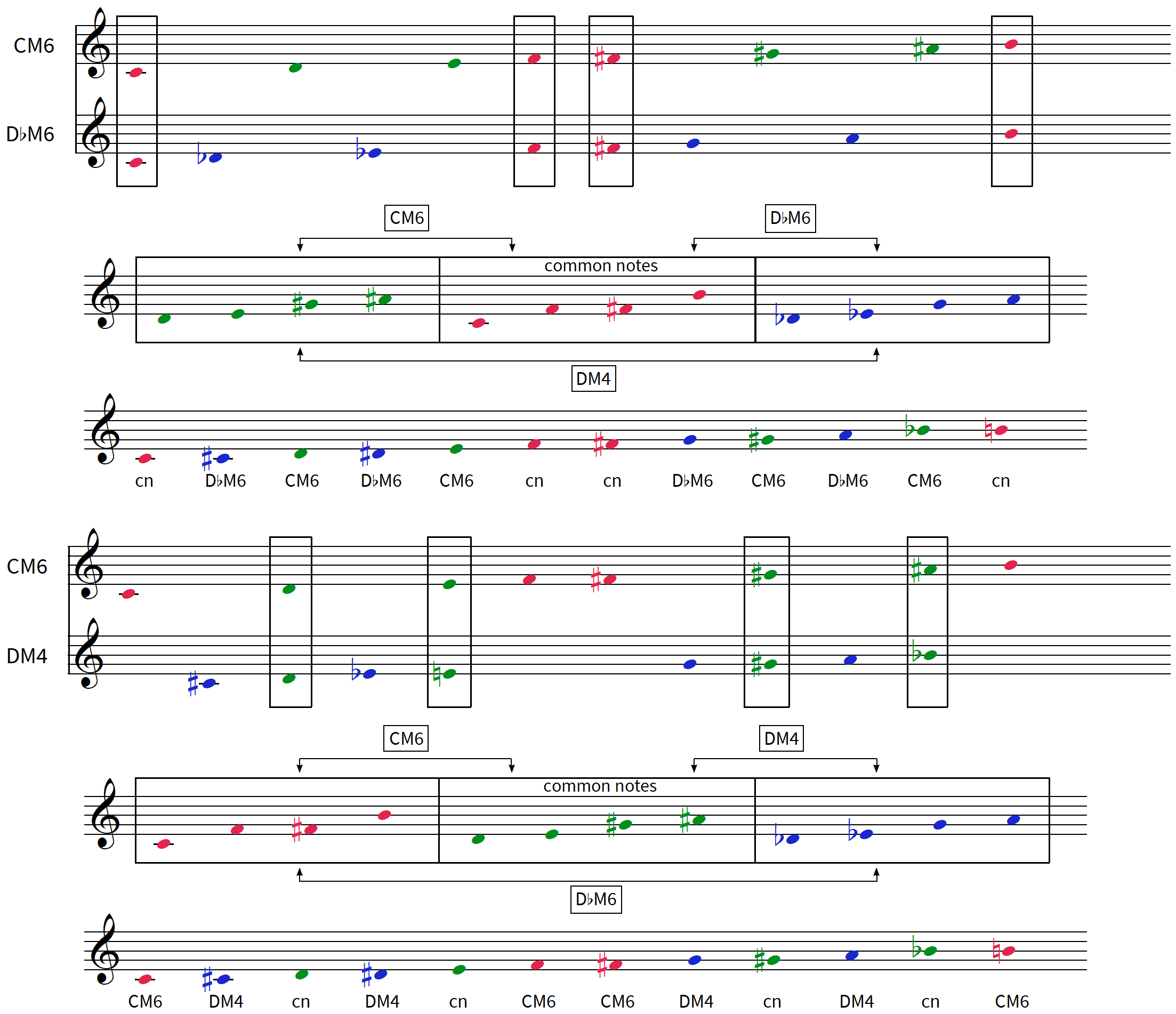
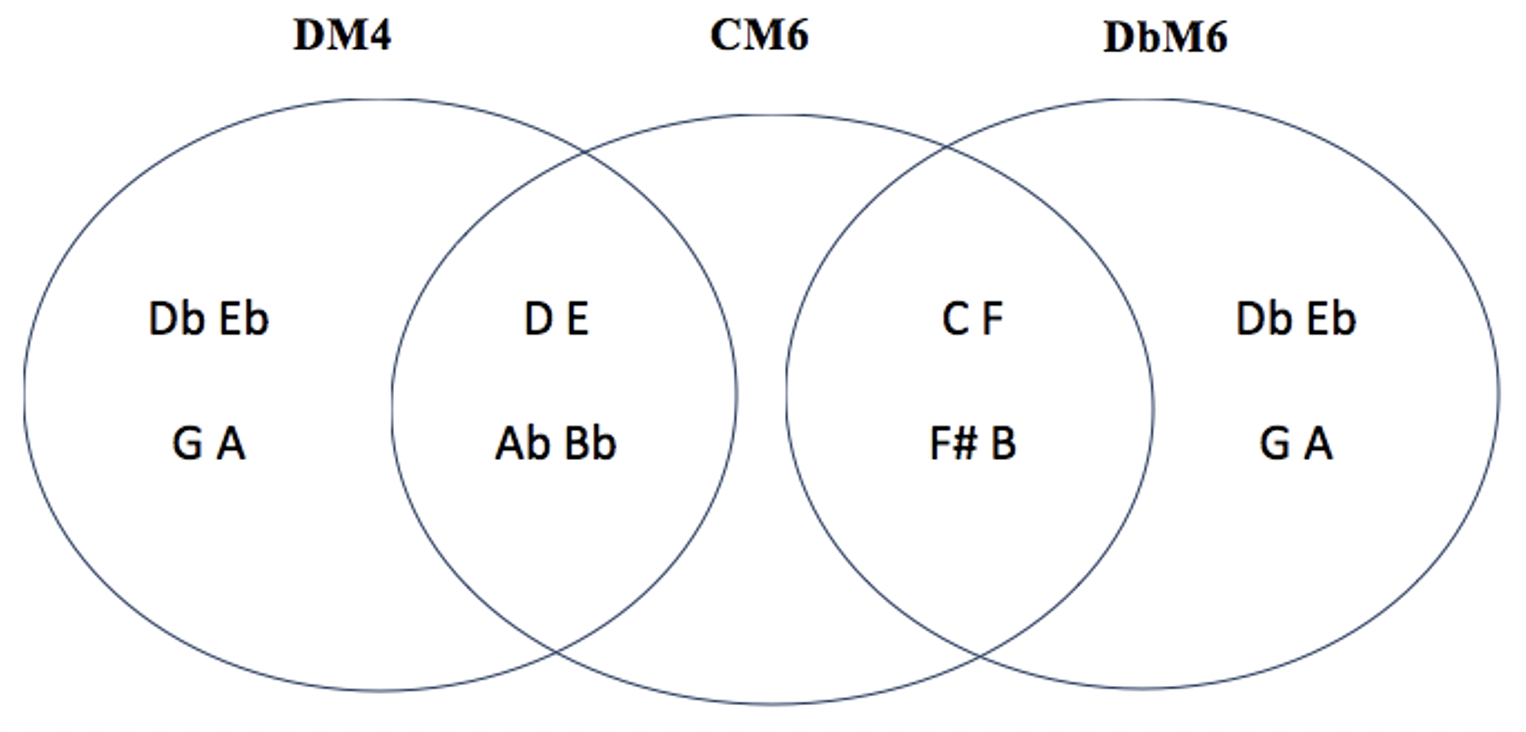
les 6 modes complémentaires de CM6 : CM2 – EbM6 / DM4 – DbM6 / DbM4 – FM6
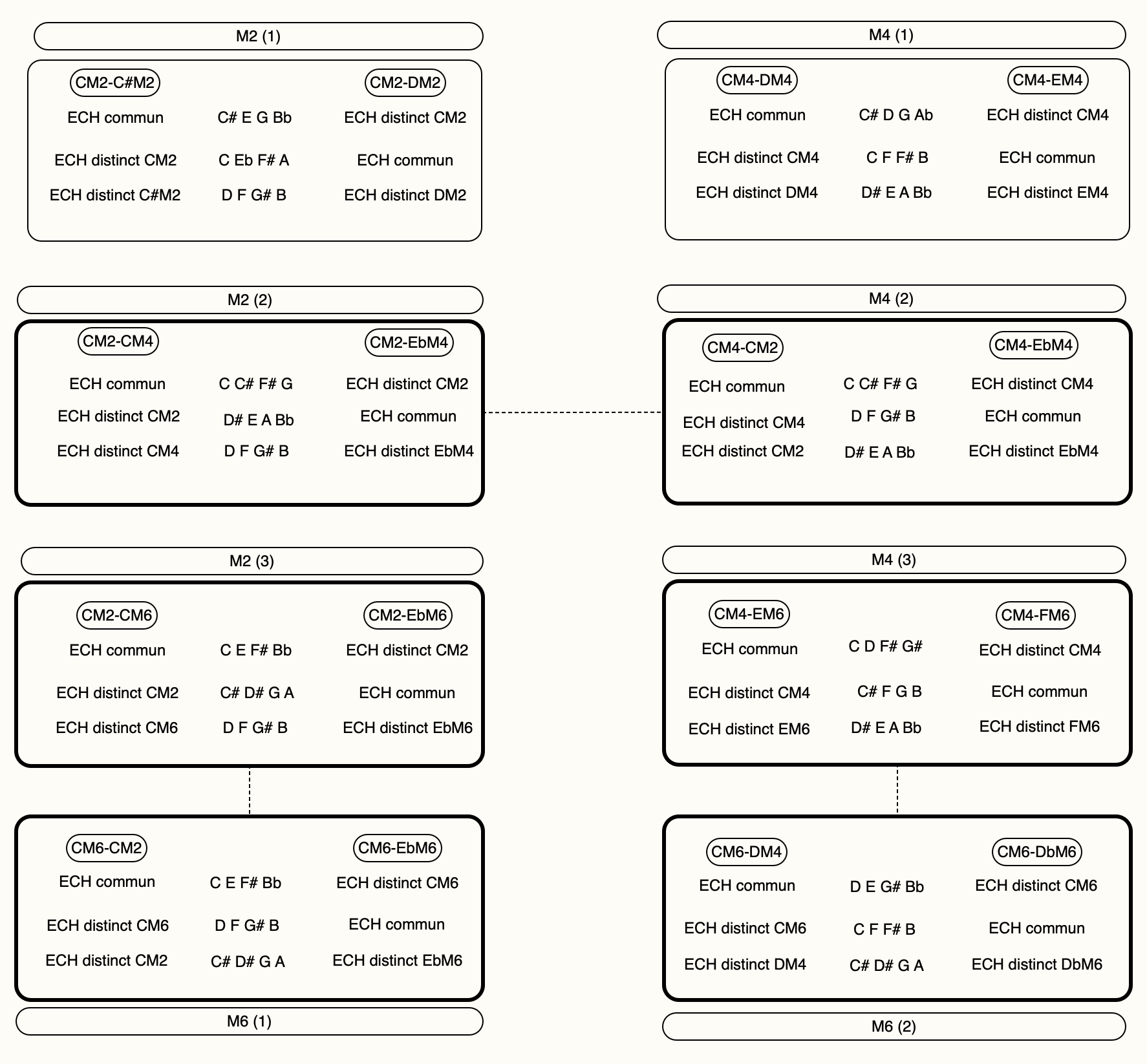
visualisation des 18 MC en satelittes orbitant autour de leurs nucleus :
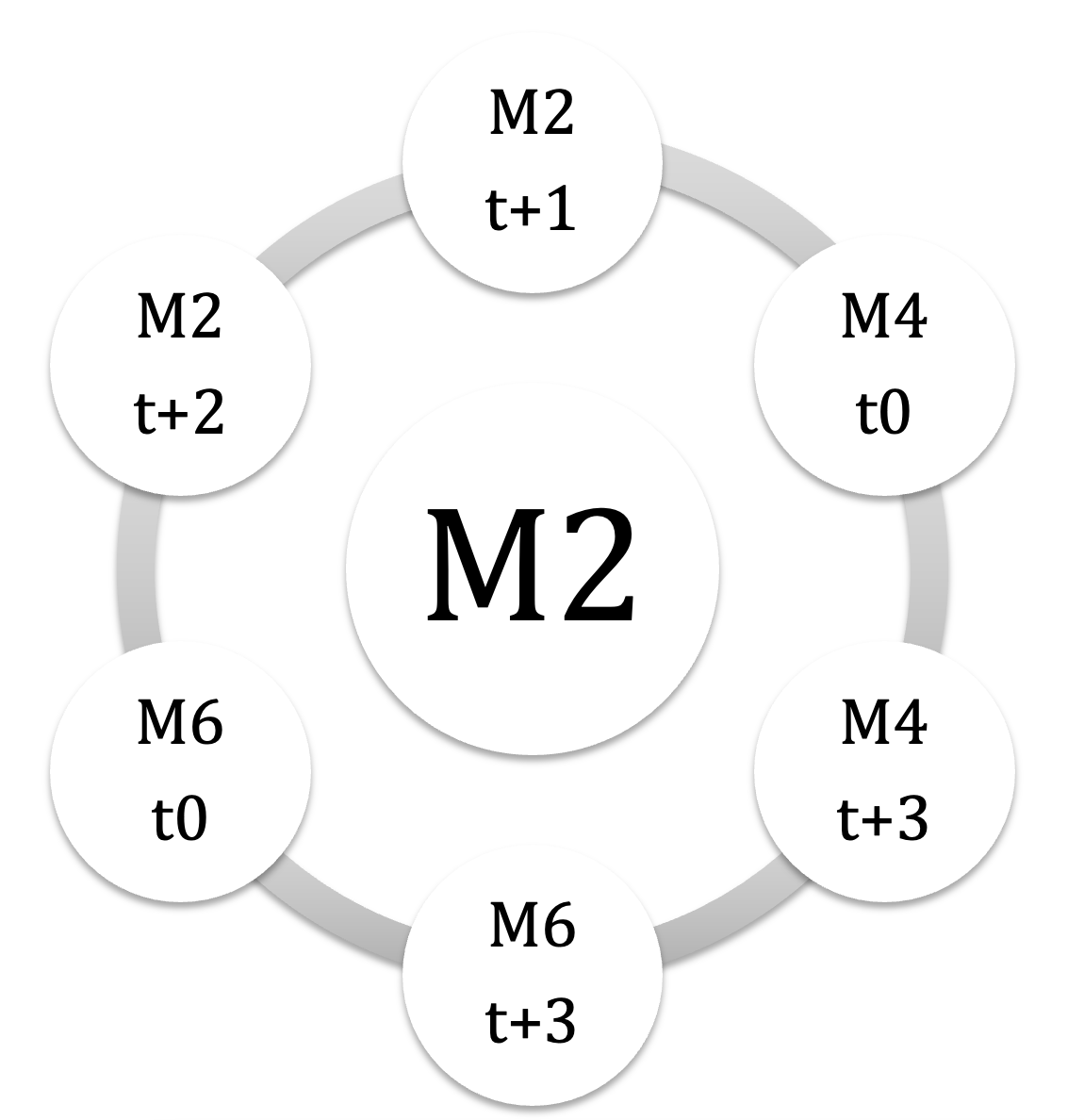
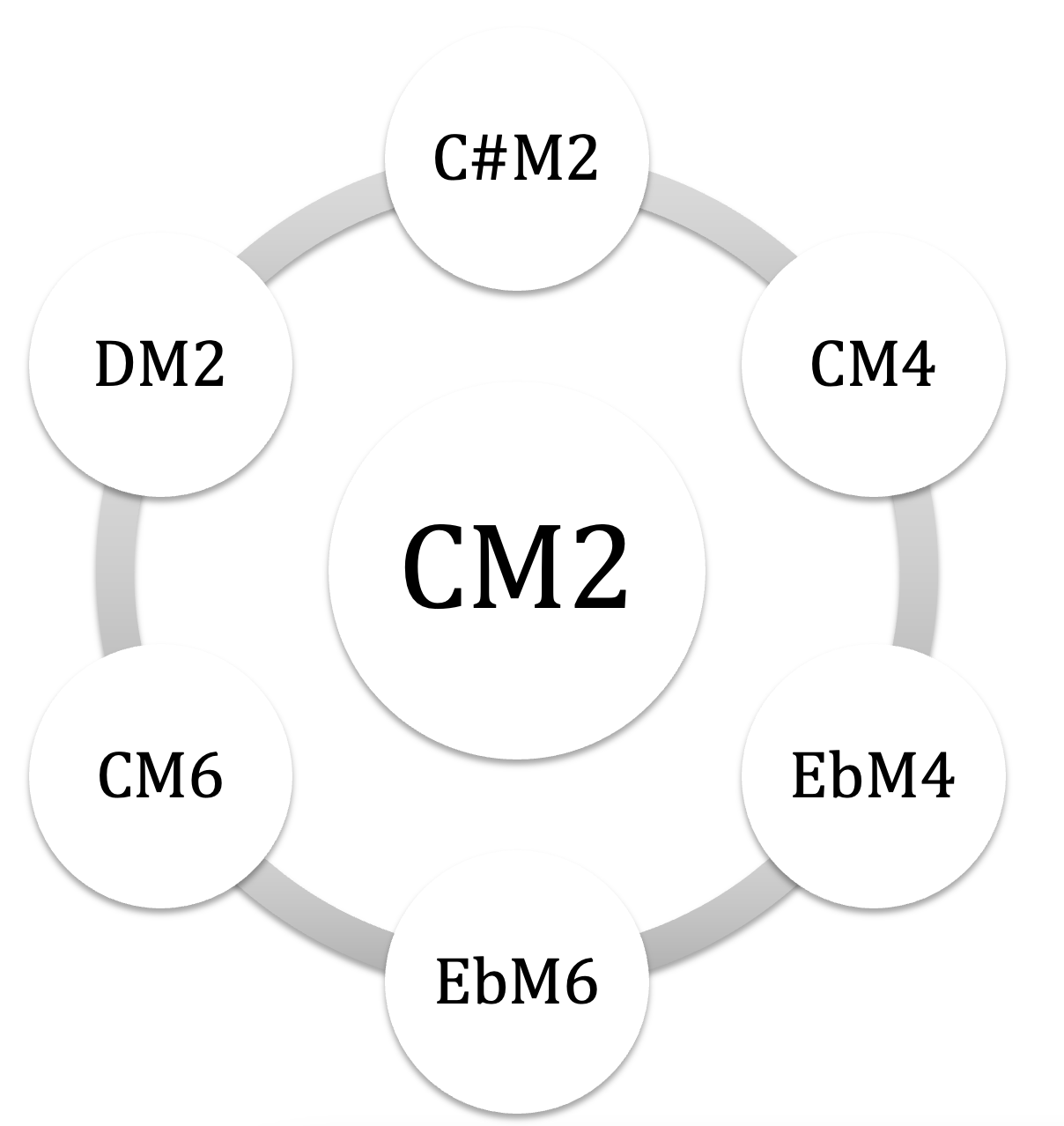
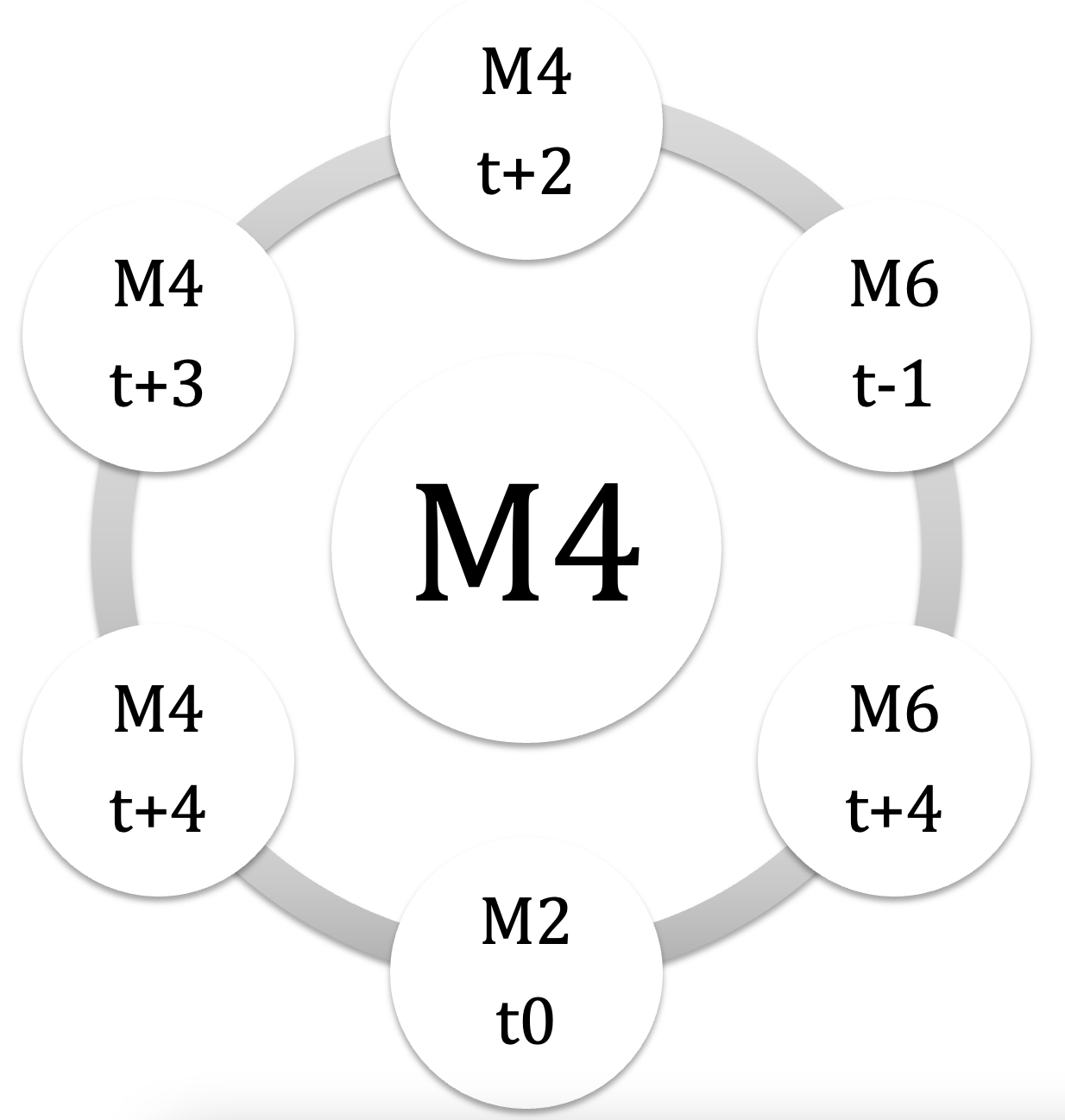
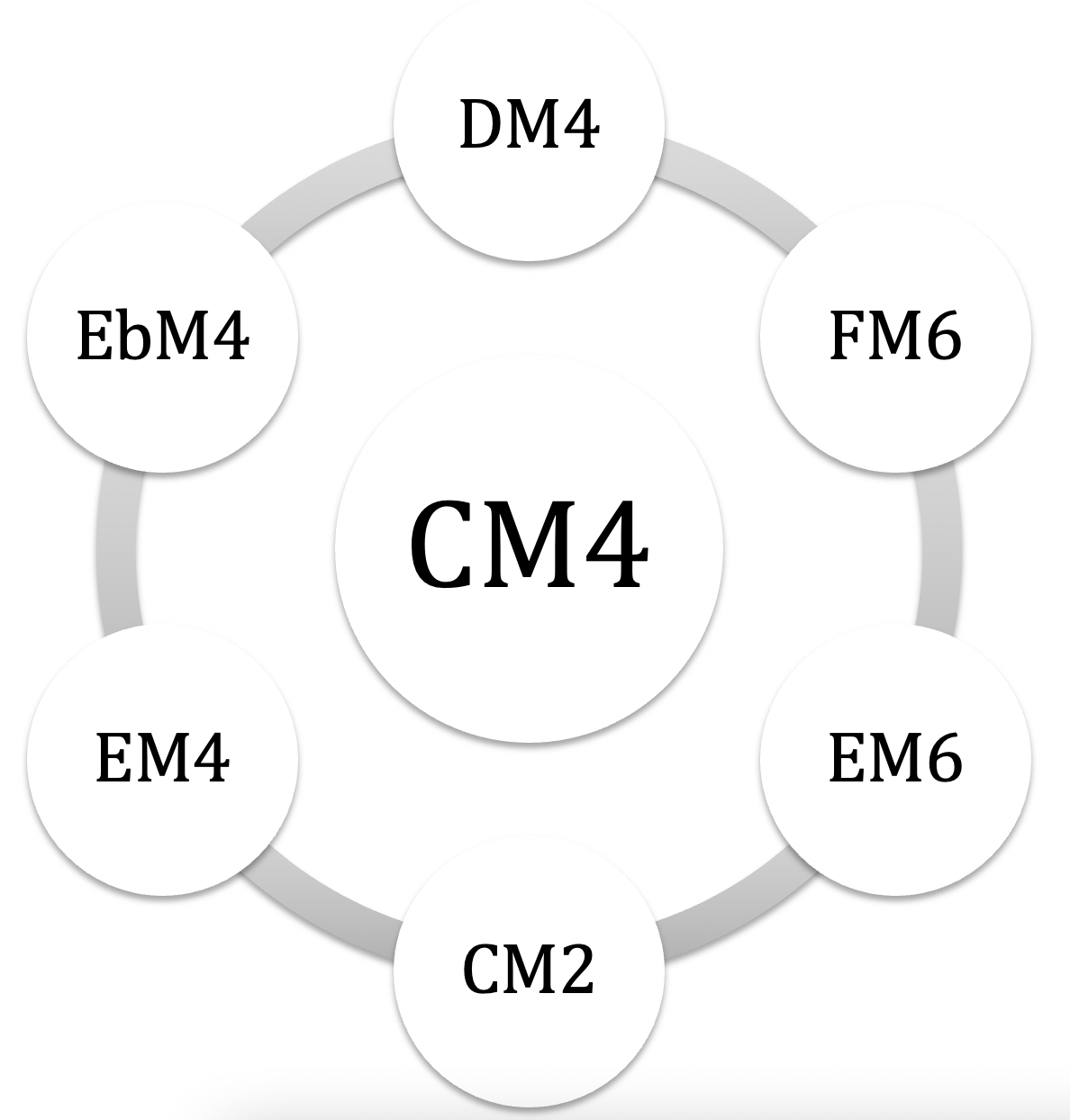
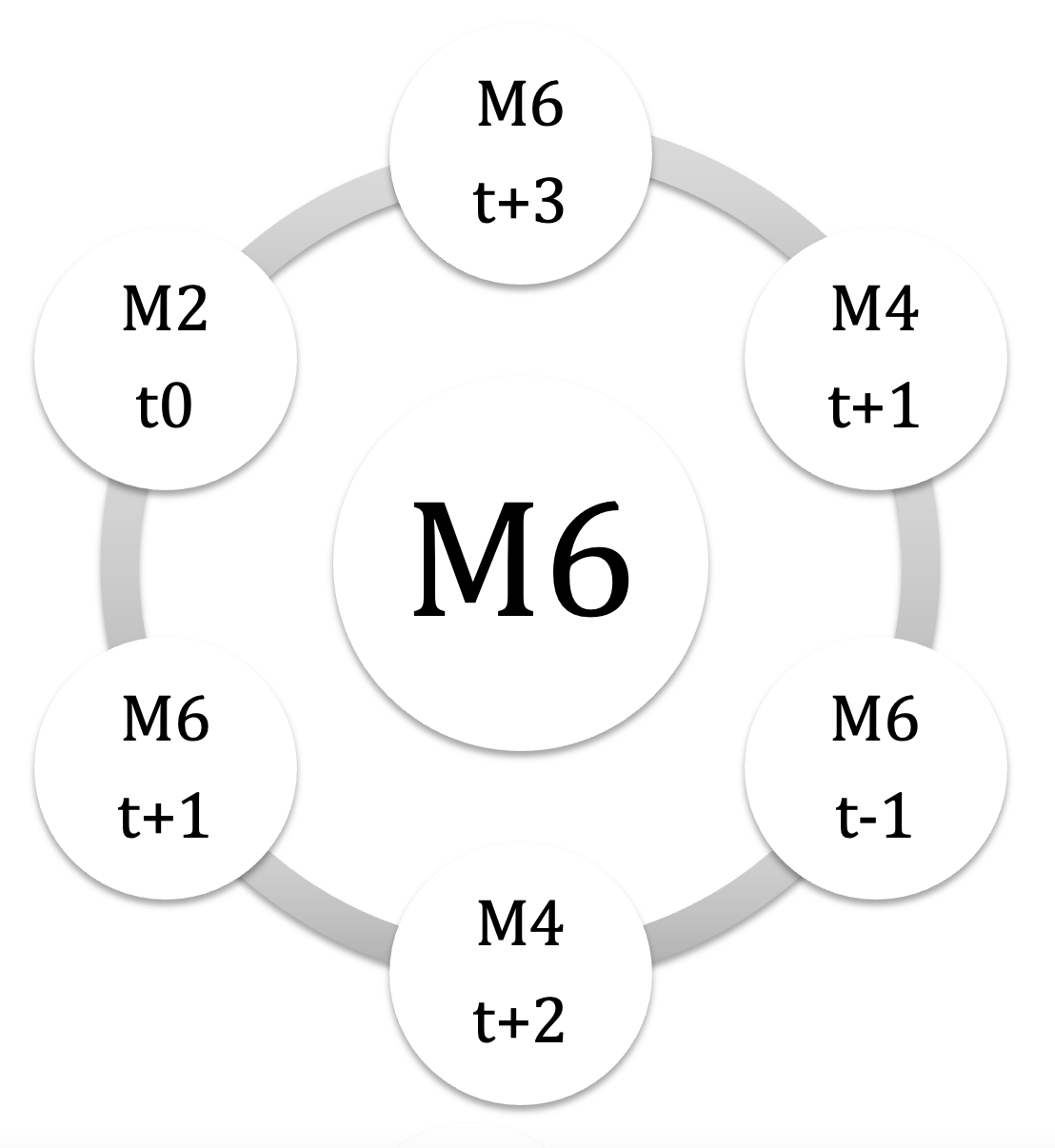
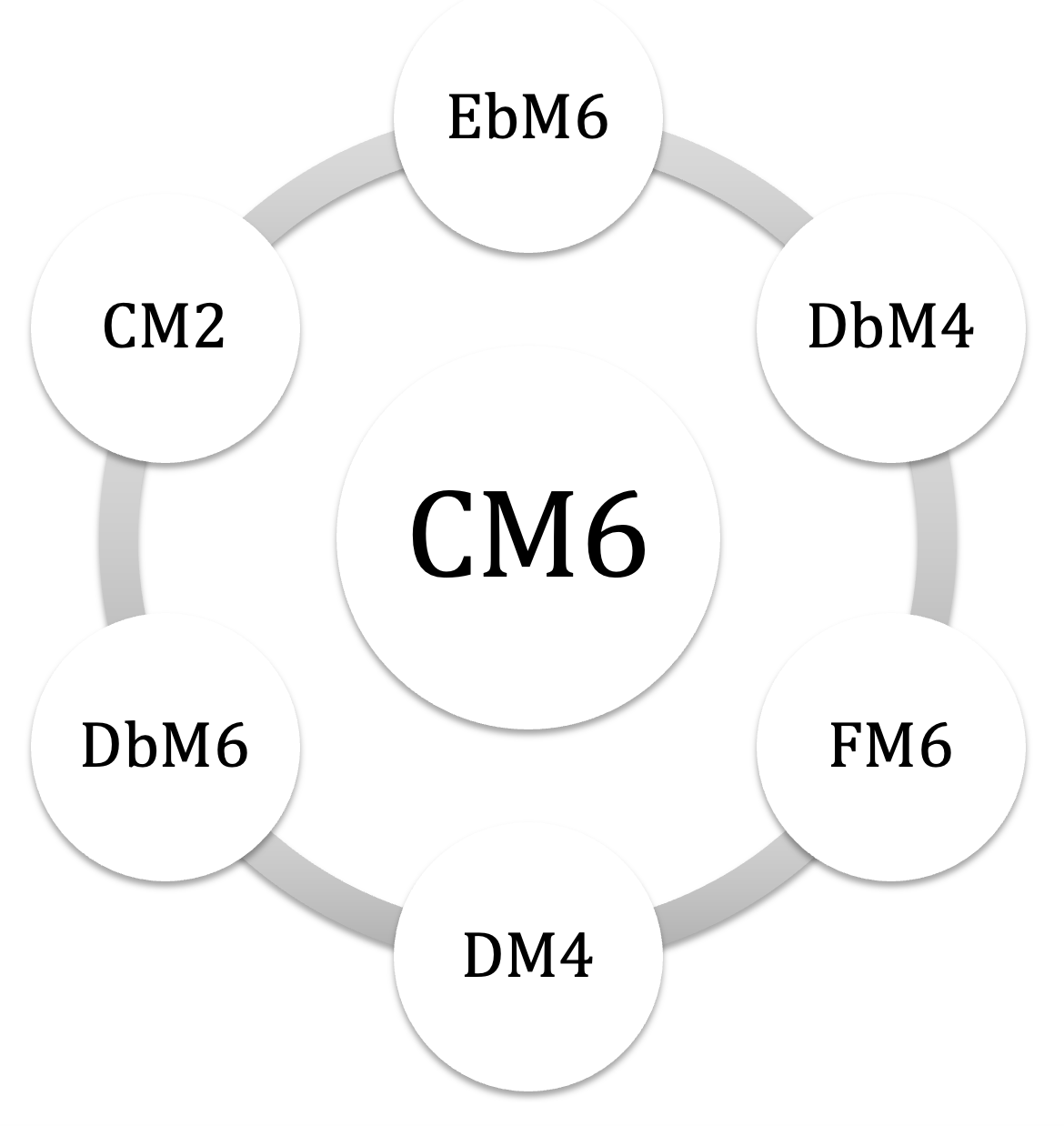
on notera que les 6 MC d’un mode donné sont eux-mêmes complémentaires 2 à 2, on peut donc visualiser la liste en regroupant les MC par ‘trilogies’
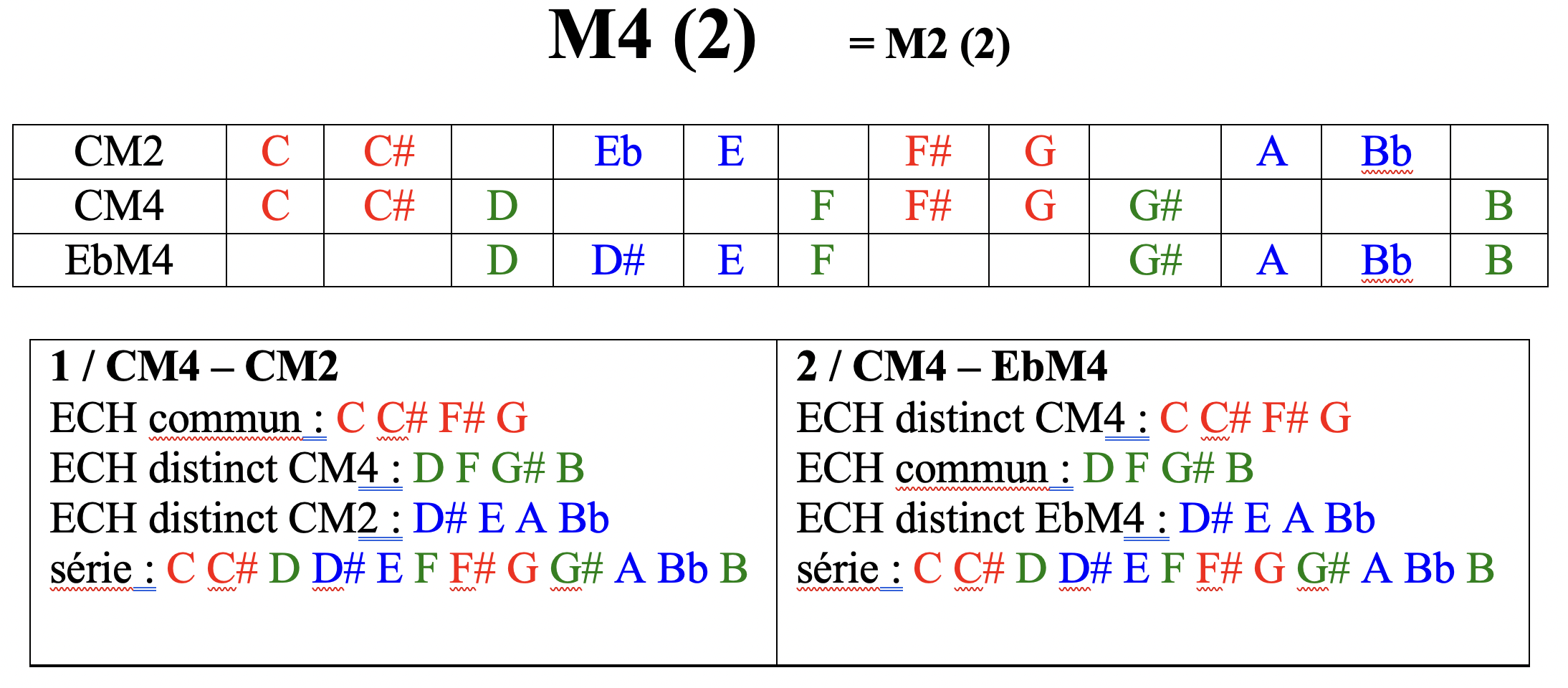
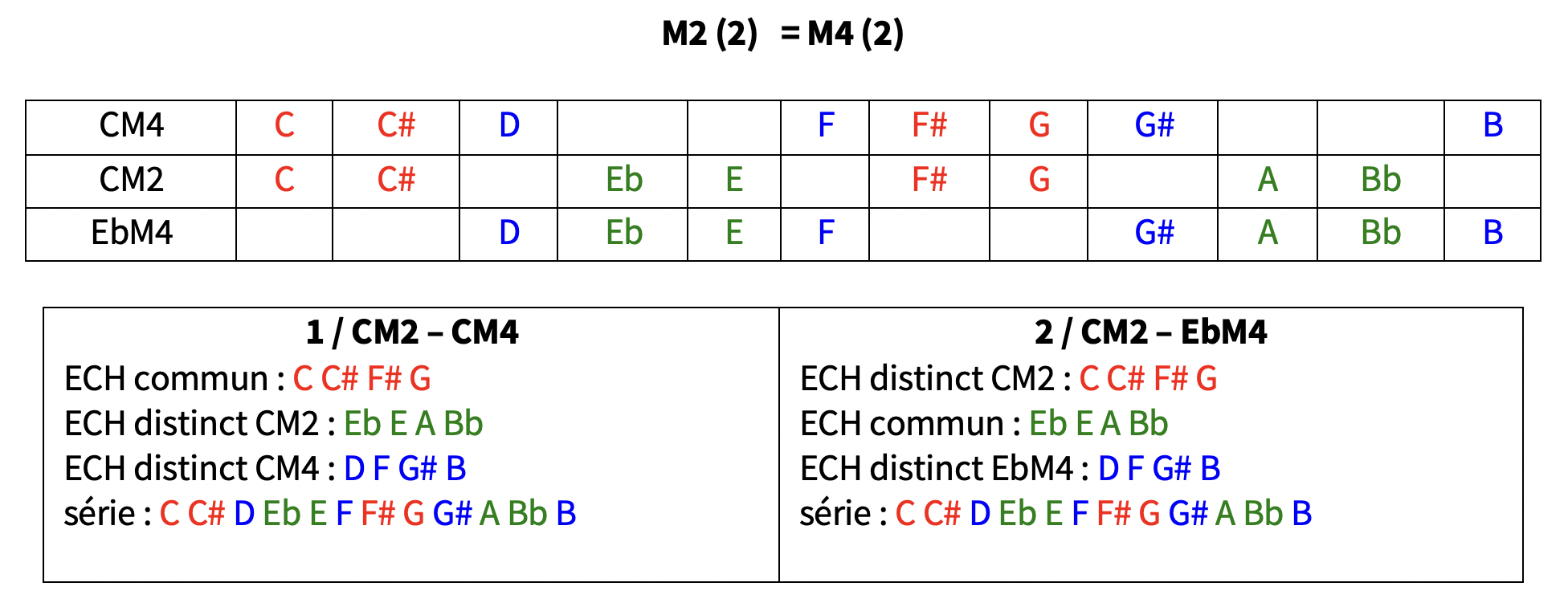
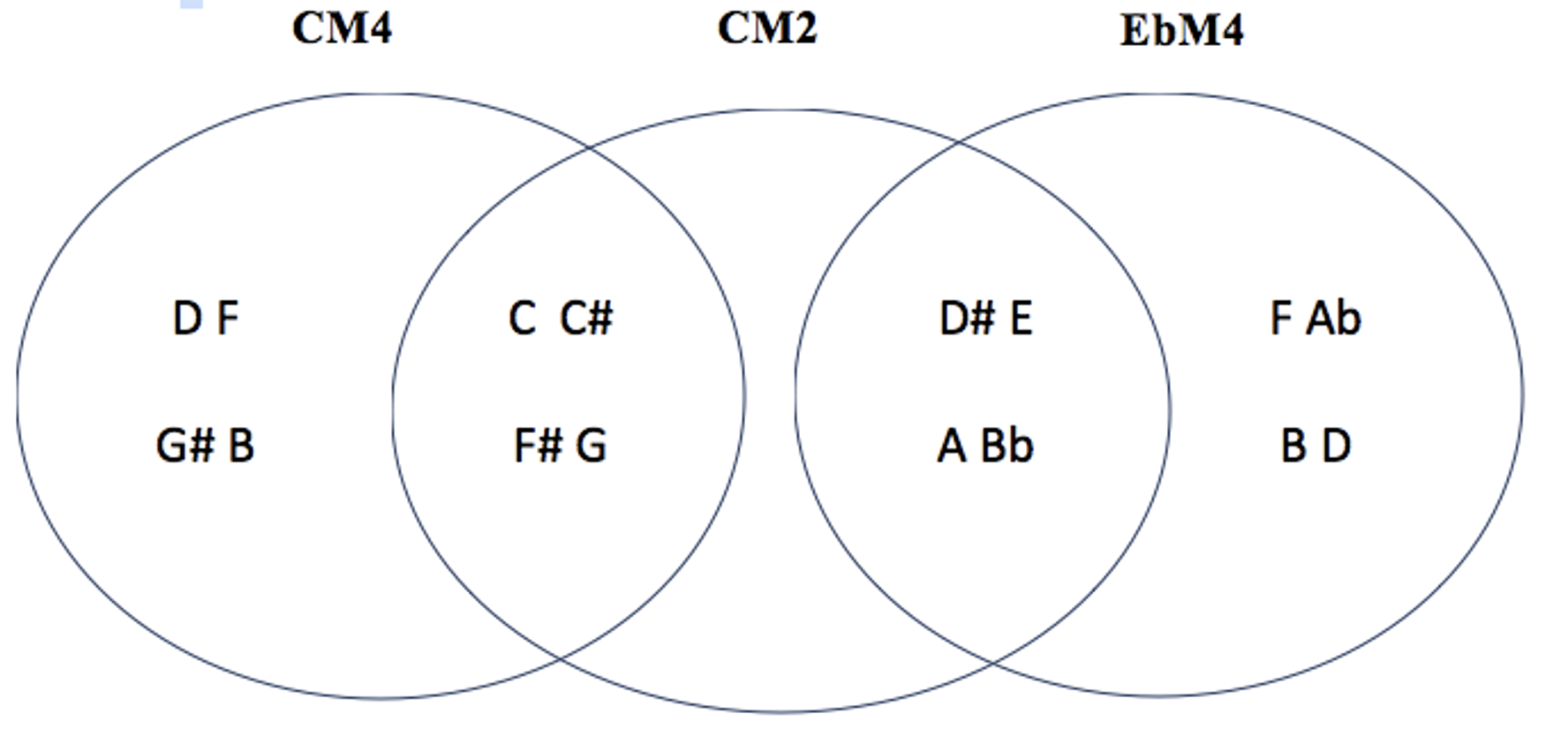
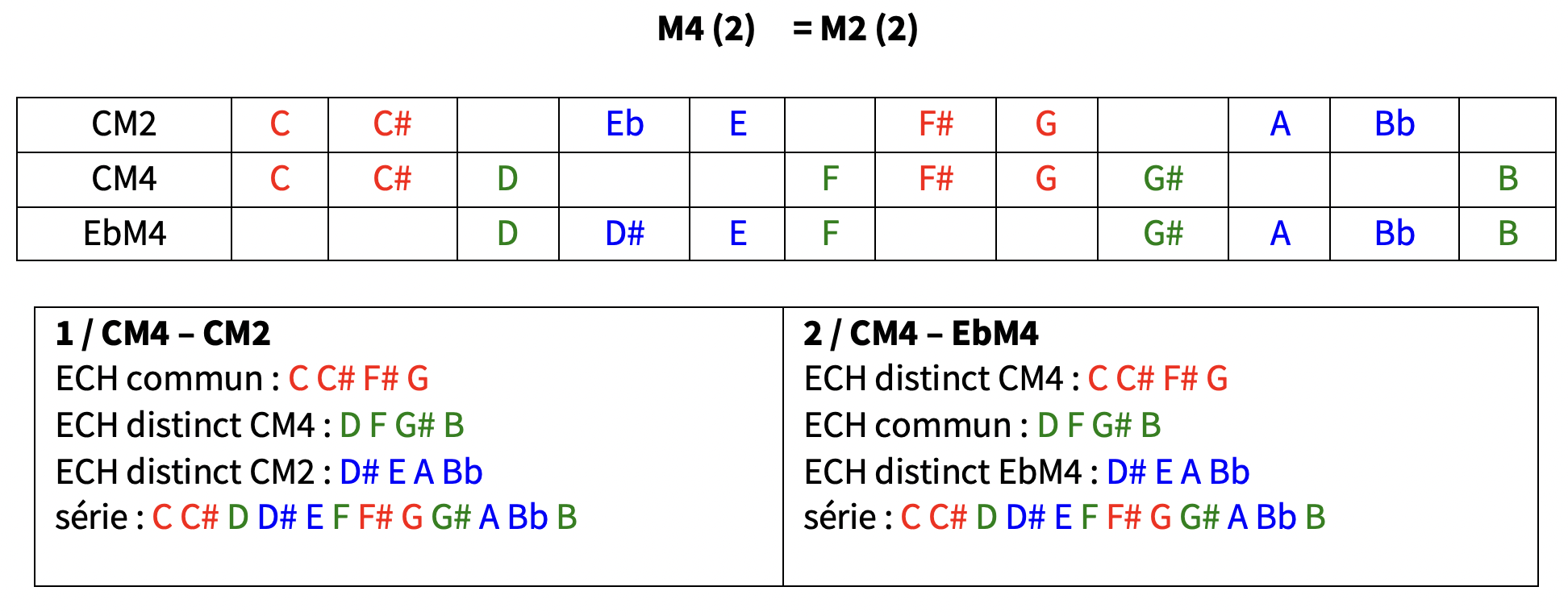
exemple pour le tableau M2 (2) : CM2-CM4 et CM2-EbM4 : CM4 et EbM4 sont complémentaires / cf M4 (2)
les 15 ‘trilogies’ complémentaires
CM2 C#M2 DM2 voir tableau M2 (1) : parce que CM2 = EbM2 = F#M2=AM2 / C#M2=EM2=GM2=BbM2 / DM2=FM2=AbM2=BM2, la trilogie CM2 C#M2 DM2 = C#M2 DM2 EbM2 = DM2 EbM2 EM2 = EbM2 EM2 FM2 = EM2 FM2 CM2 = FM2 CM2 C#M2
CM2 CM4 EbM4
C#M2 C#M4 EM4
DM2 DM4 FM4 voir tableau M2 (2) / M4 (2)
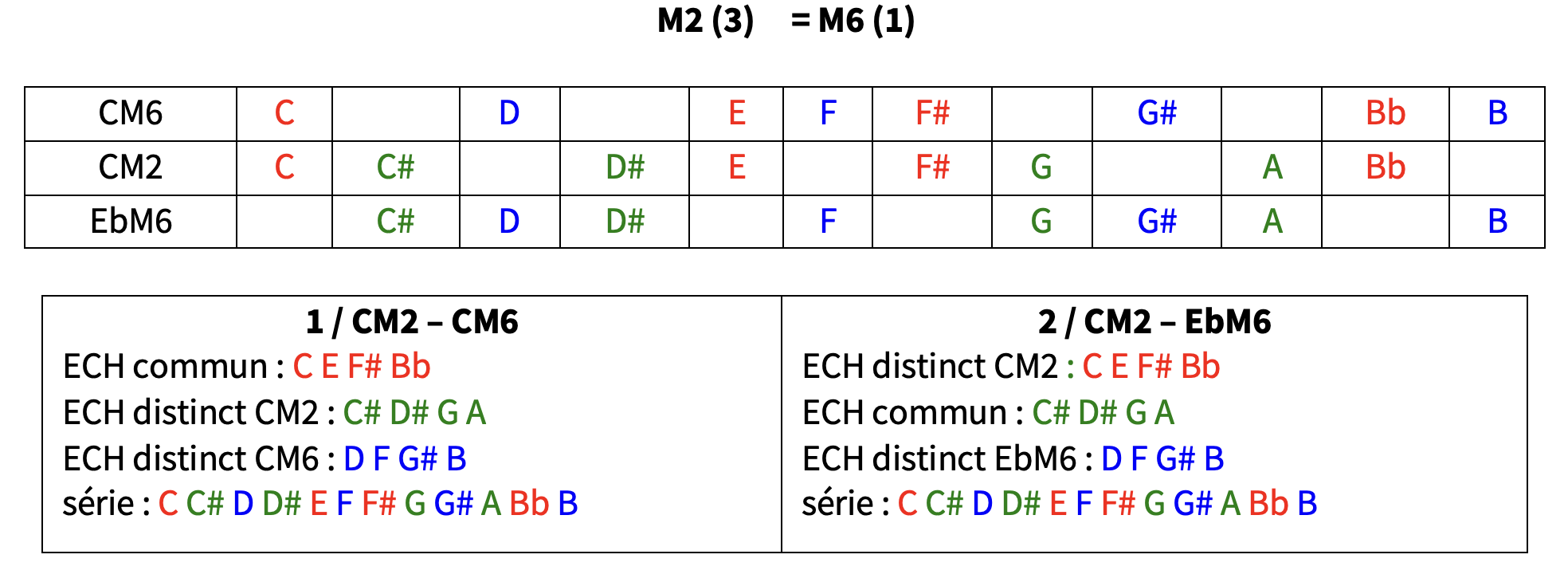
CM2 CM6 EbM6
C#M2 C#M6 EM6
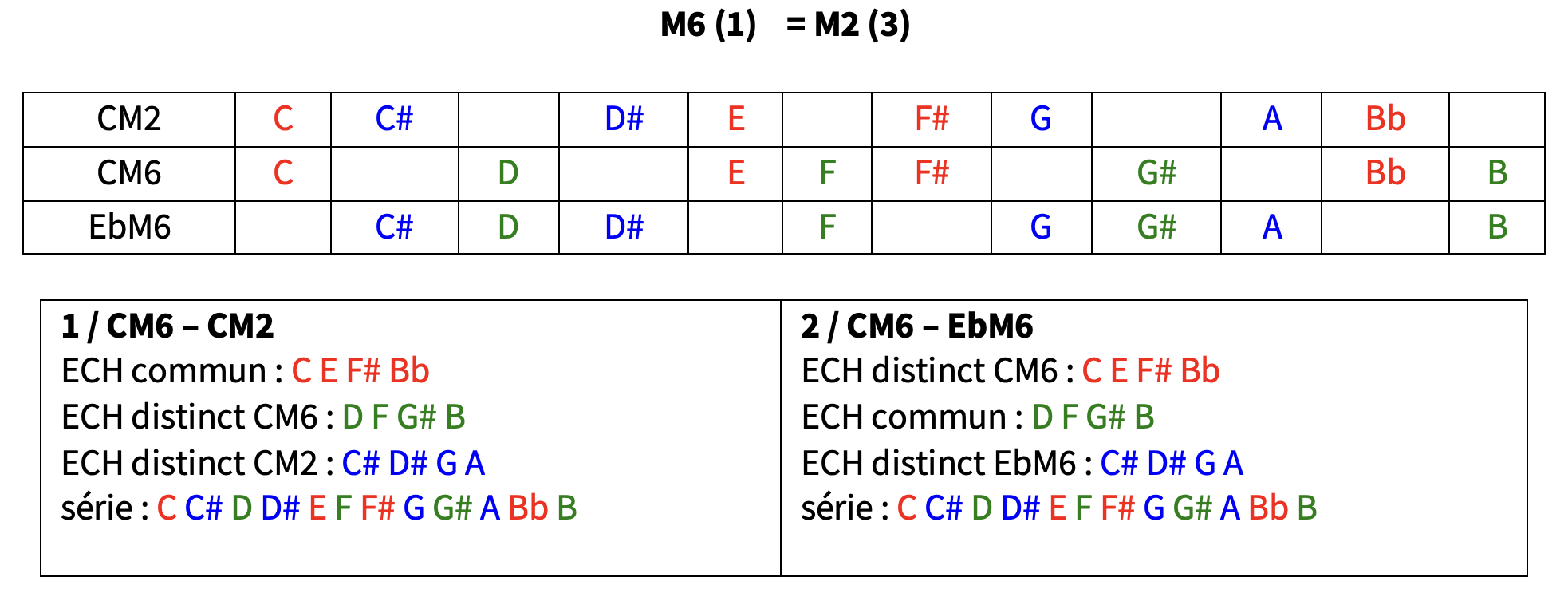
DM2 DM6 FM6 voir tableau M2 (3) / M6 (1)
CM4 DM4 EM4
C#M4 EbM4 FM4 voir tableau M4 (1)
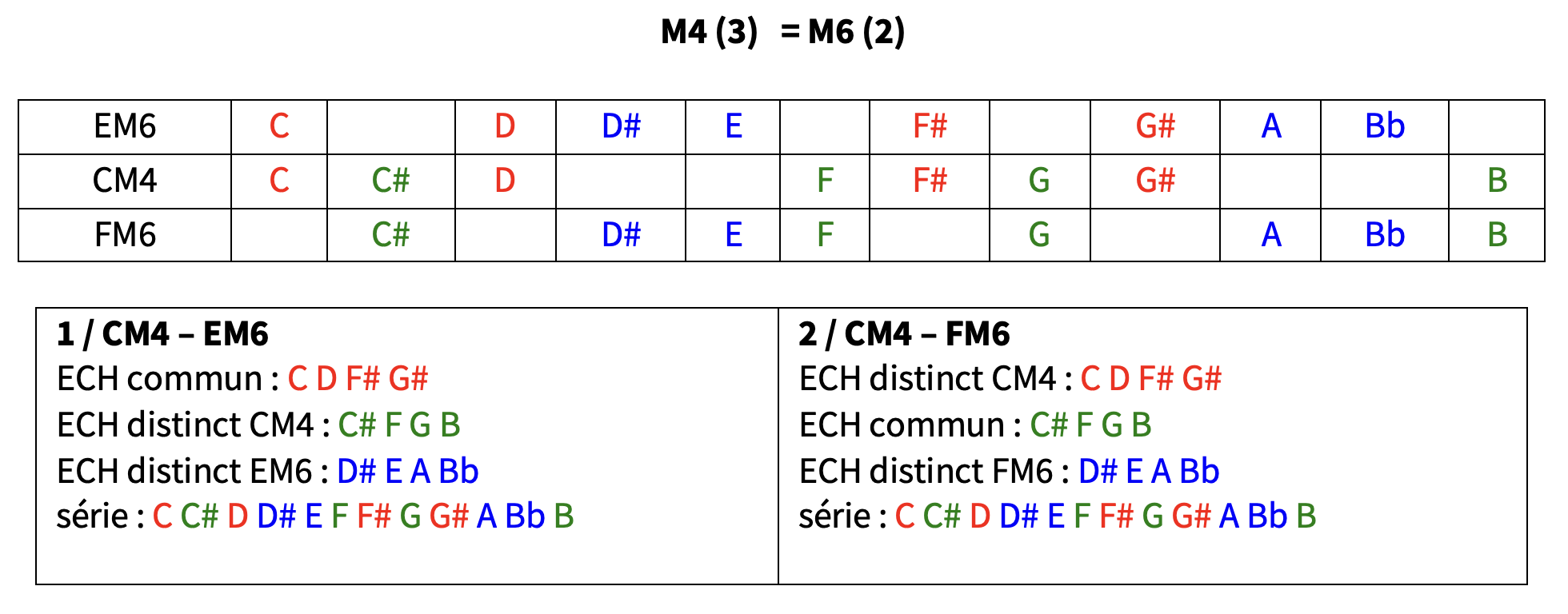
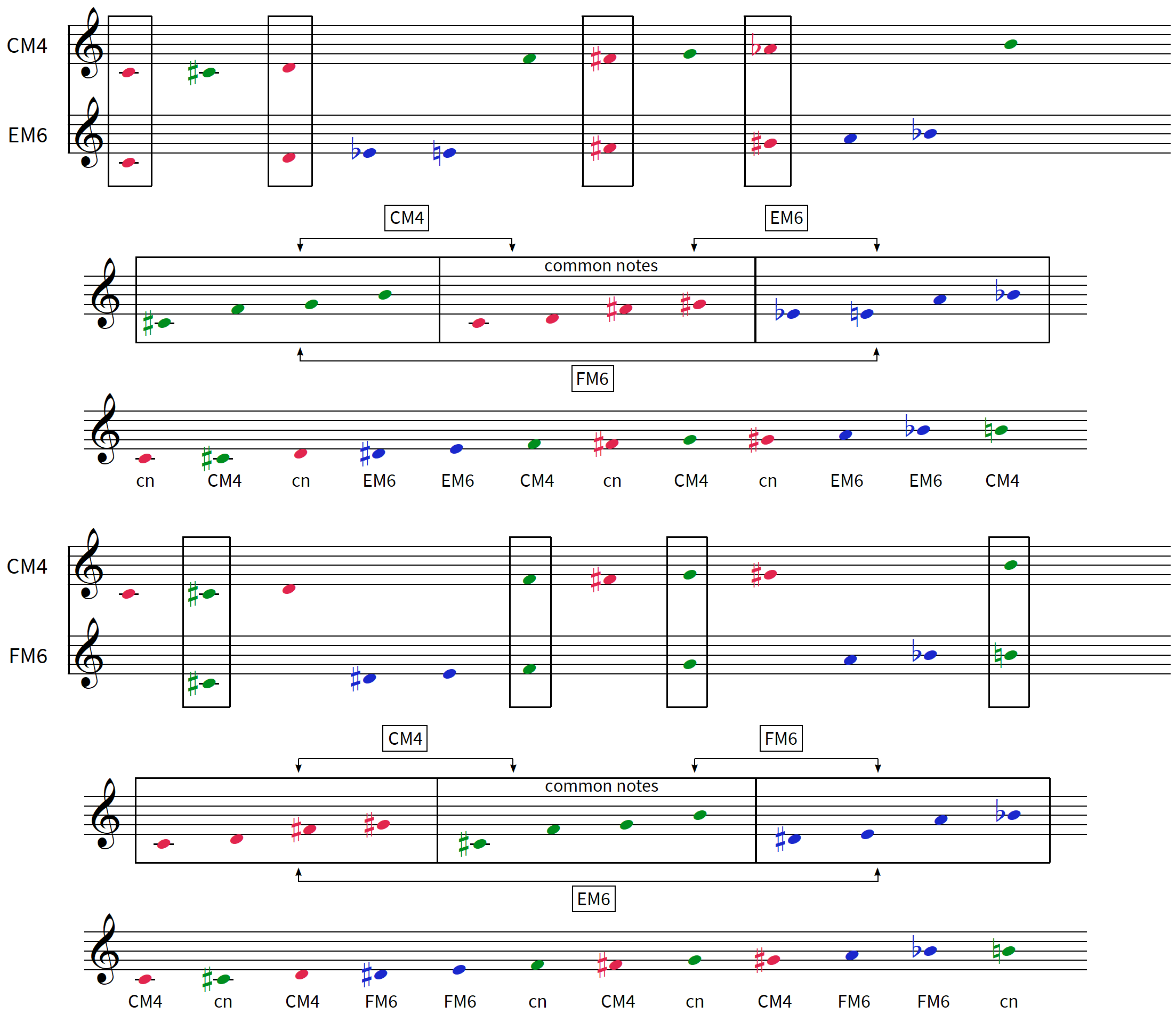
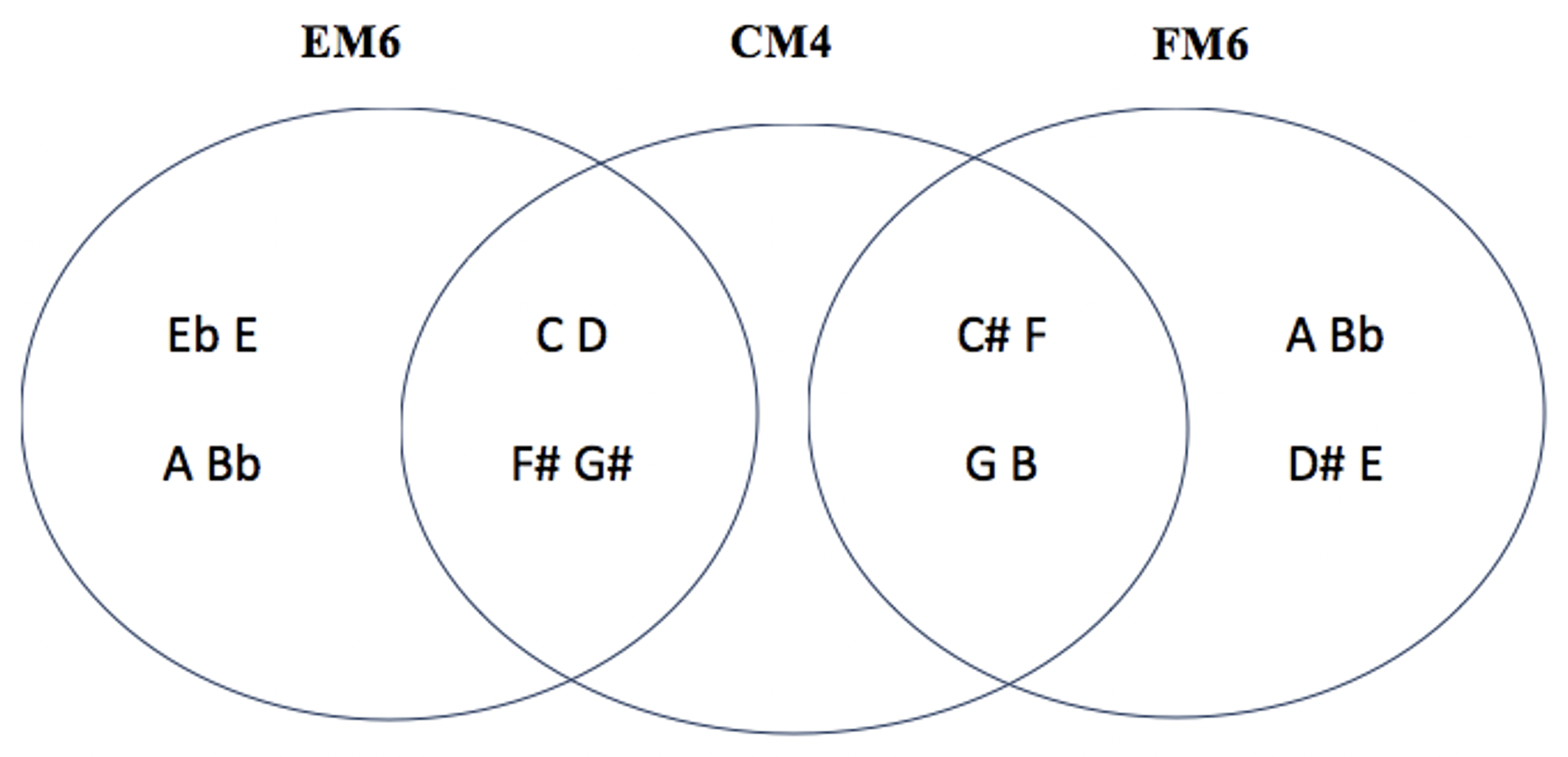
CM4 EM6 FM6
C#M4 FM6 CM6
DM4 CM6 C#M6
EbM4 C#M6 DM6
EM4 DM6 EbM6
FM4 EbM6 EM6 voir tableau M4 (3) / M6 (2)


( pour une vue complète des trilogies complémentaires, on fera le même tableau pour les 2 trilogies apparentées t+1 et t+2 : C#M2 C#M4 EM4 et DM2 DM4 FM4 ) ( nb: si on continue le cycle des transpositions: t+3 = EbM2(=CM2) EbM4 F#M4 (=CM4) , identique à la trilogie de départ CM2 CM4 EbM4 )
( pour obtenir une liste complète des trilogies complémentaires, on fera le même tableau pour les 2 trilogies apparentées t+1 et t+2 : C#M2 C#M6 EM6 et DM2 DM6 FM6 ) ( nb: si on continue le cycle des transpositions: t+3 = EbM2(=CM2) EbM6 F#M6 (=CM6) , identique à la trilogie de départ CM2 CM6 EbM6 )
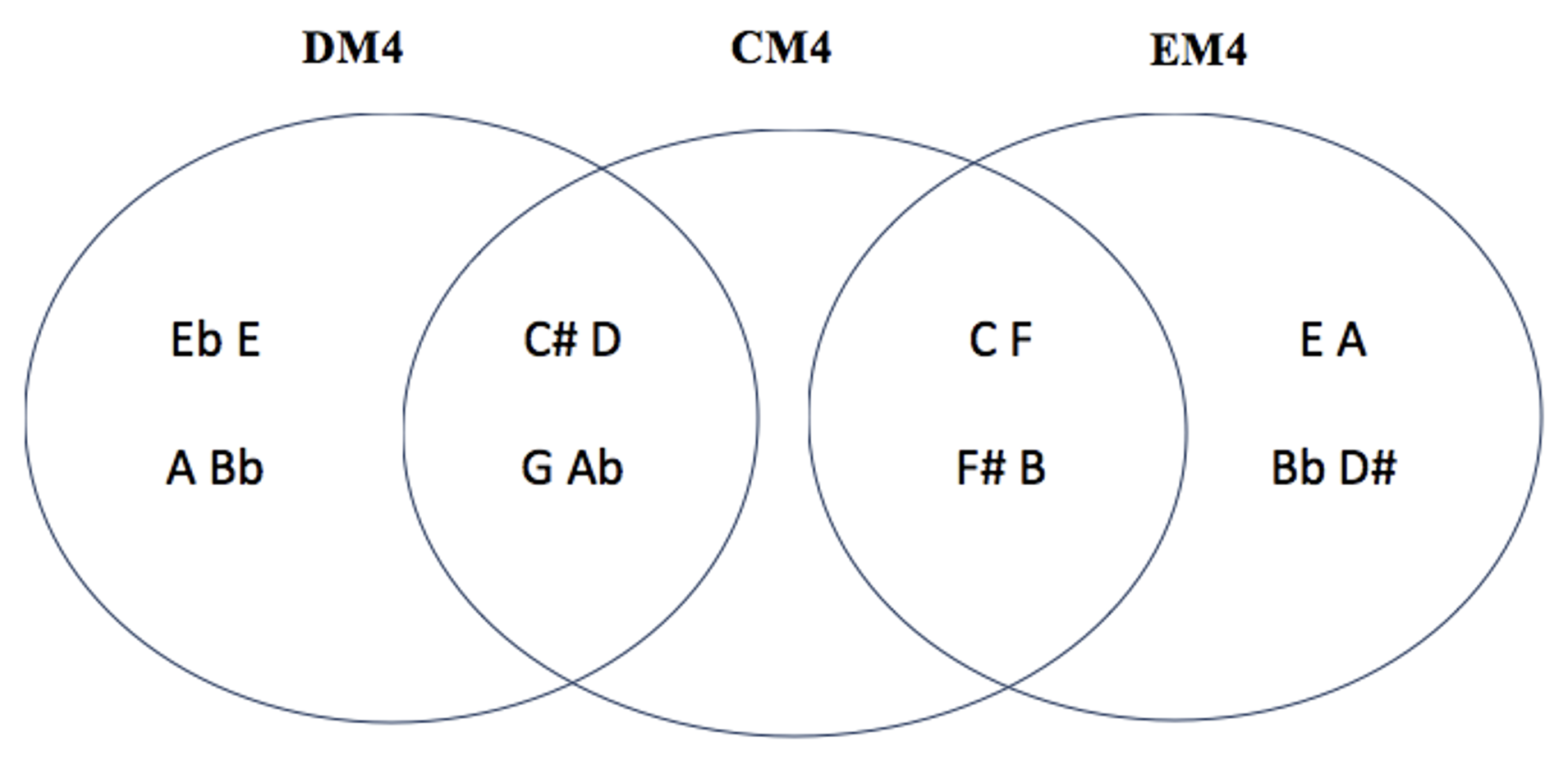
( pour une vue complète des trilogies complémentaires, on fera le même tableau pour la trilogie apparentée t+1 : C#M4 EbM4 FM4 ) ( nb: si on continue le cycle des transpositions: t+2 = DM4 EM4 F#M4 (=CM4) , identique à la trilogie de départ CM4 DM4 EM4 )
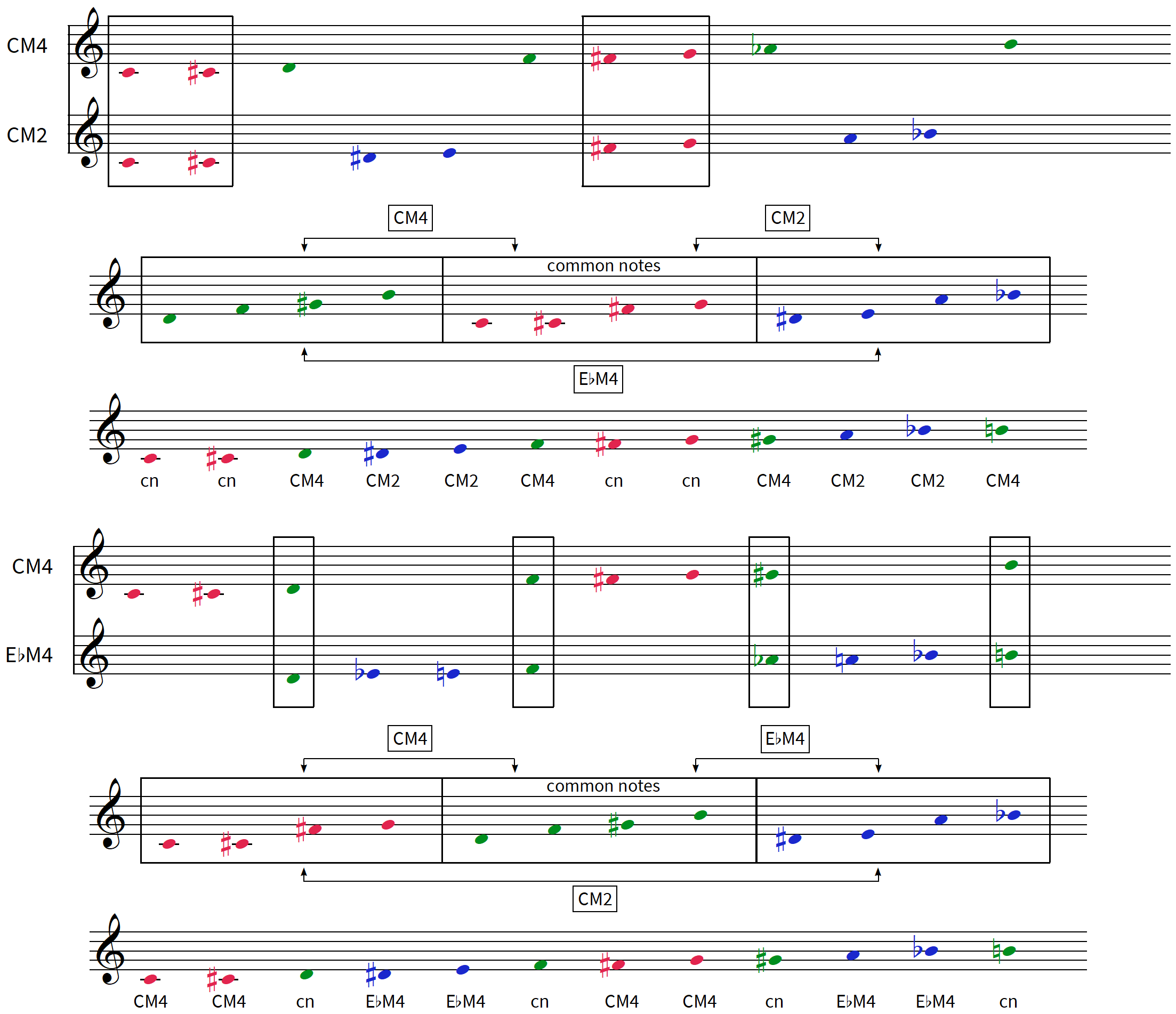
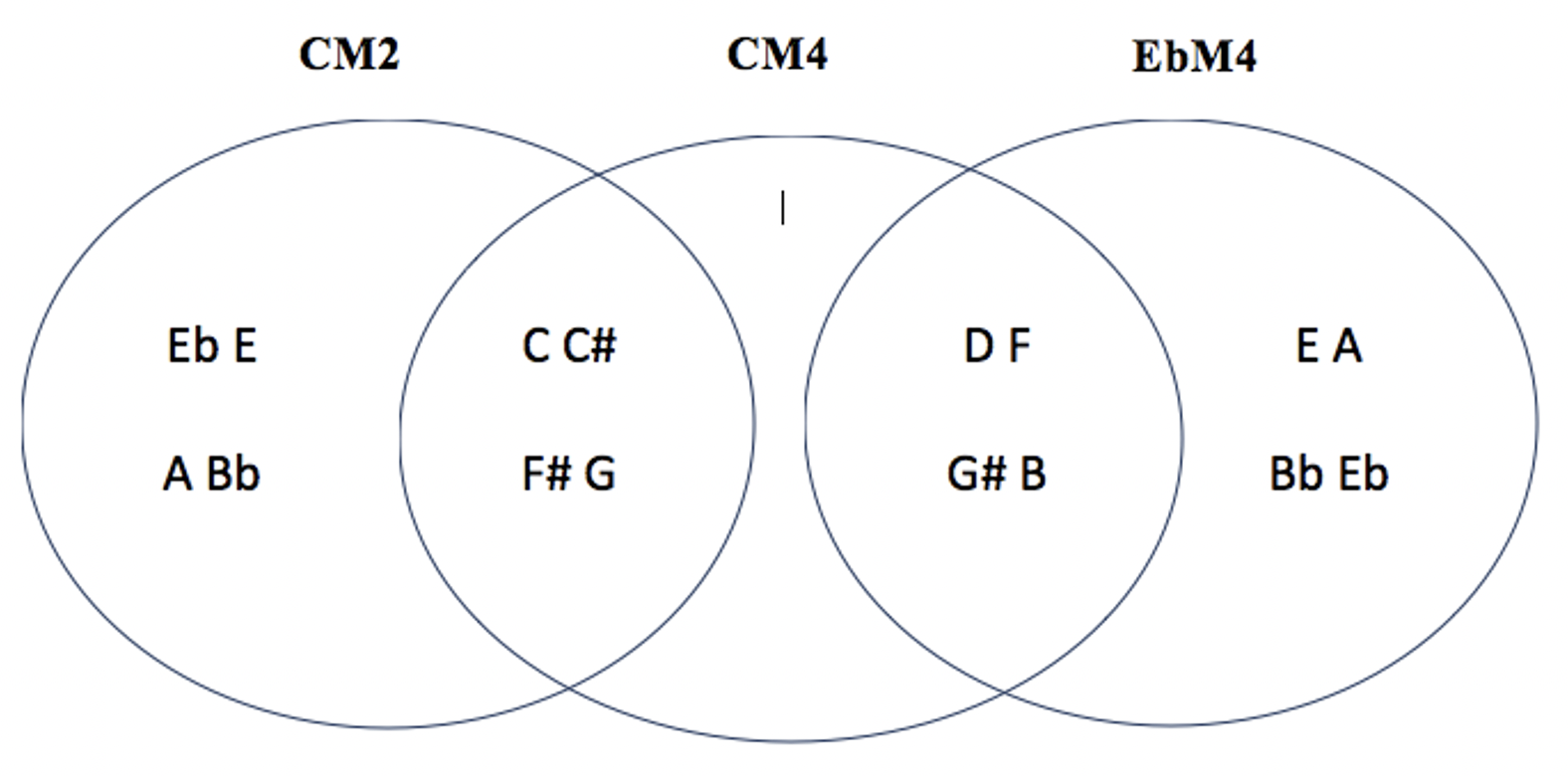
pour une vue complète des trilogies complémentaires on fera le même tableau pour les 2 trilogies apparentées t+1 et t+2: C#M4 C#M2 EM4 / DM4 DM2 FM4 ( nb: si on continue le cycle des transpositions: t+3 = EbM4 EbM2 (=CM2) F#M4 (=CM4) , identique à la trilogie de départ CM4 CM2 EbM4 )
( pour une vue complète des trilogies complémentaires, on fera le même tableau pour les trilogies apparentées t+1, t+2, t+3, t+4 et t+5 : C#M4 FM6 CM6 / DM4 CM6 C#M6 / EbM4 C#M6 DM6 / EM4 DM6 EbM6 / FM4 EbM6 EM6 )
( pour une vue complète des trilogies complémentaires, on fera le même tableau pour les trilogies apparentées t+1et t+2 : C#M6 C#M2 EM6 et DM6 DM2 FM6 ( nb: si on continue le cycle des transpositions: t+3 = EbM6 EbM2 (=CM2) F#M6 (=CM6), identique à la trilogie de départ CM6 CM2 EbM2 )
( pour une vue complète des trilogies complémentaires, on fera le même tableau pour les trilogies apparentées t+1, t+2, t+3, t+4 et t+5 : C#M6 EbM4 DM6 / DM6 EM4 EbM6 / EbM6 FM4 EM6 / EM6 CM4 FM6 / FM6 C#M4 CM6
2 visions plus compactes ( modes complémentaires en binomes / ECH = PCset) :
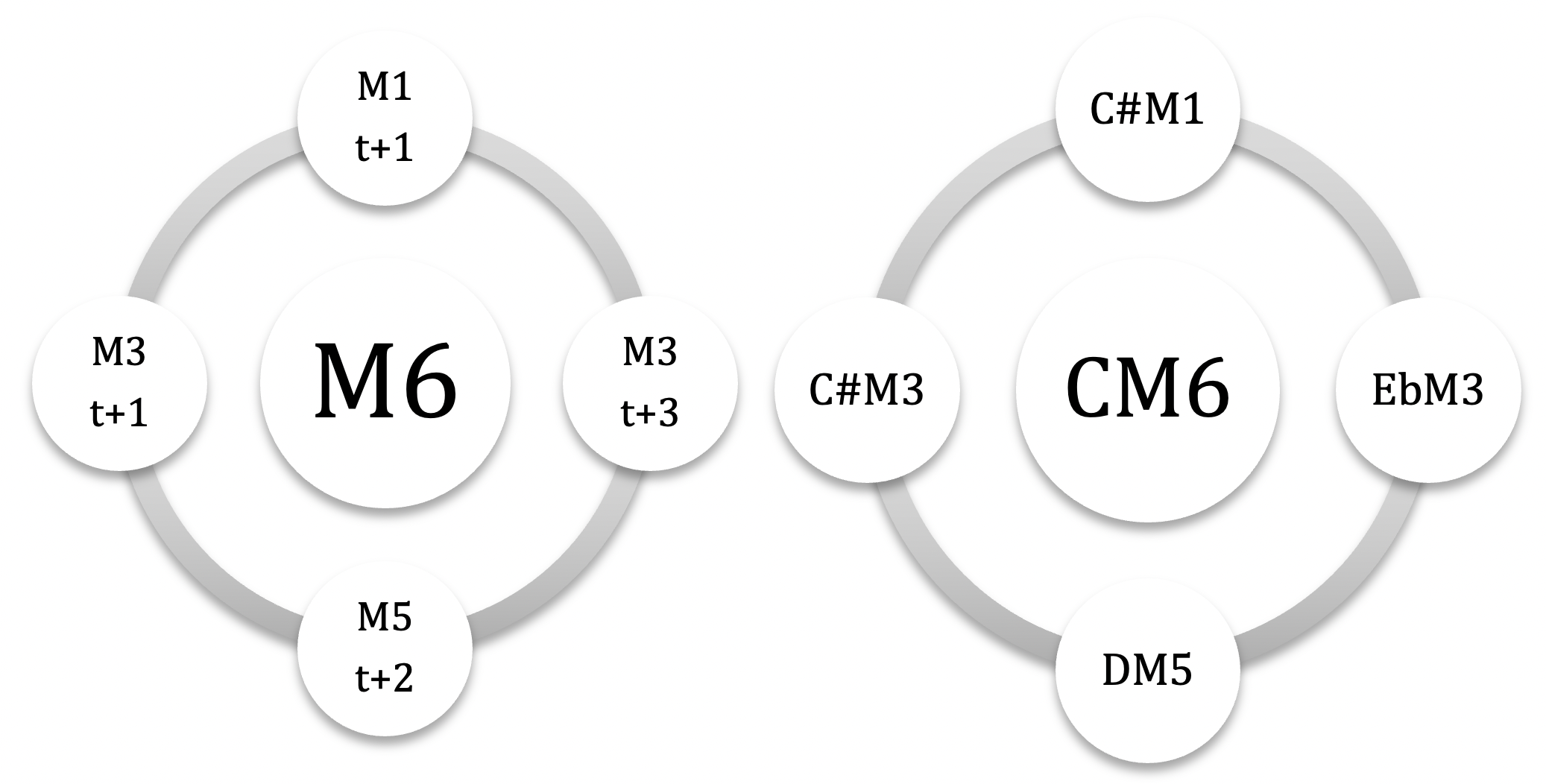
modes complémentaires ( ‘irréguliers’ : MCi )
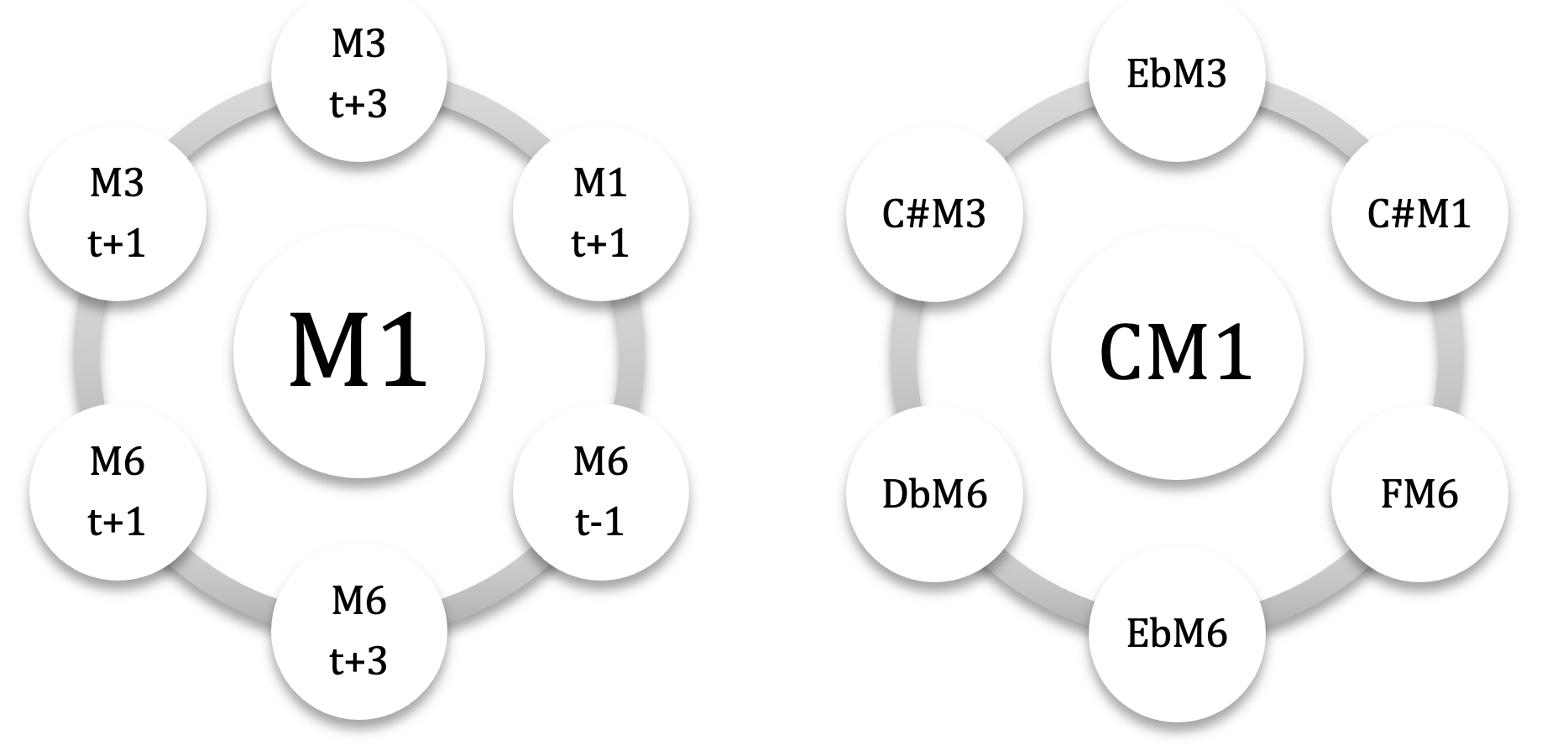
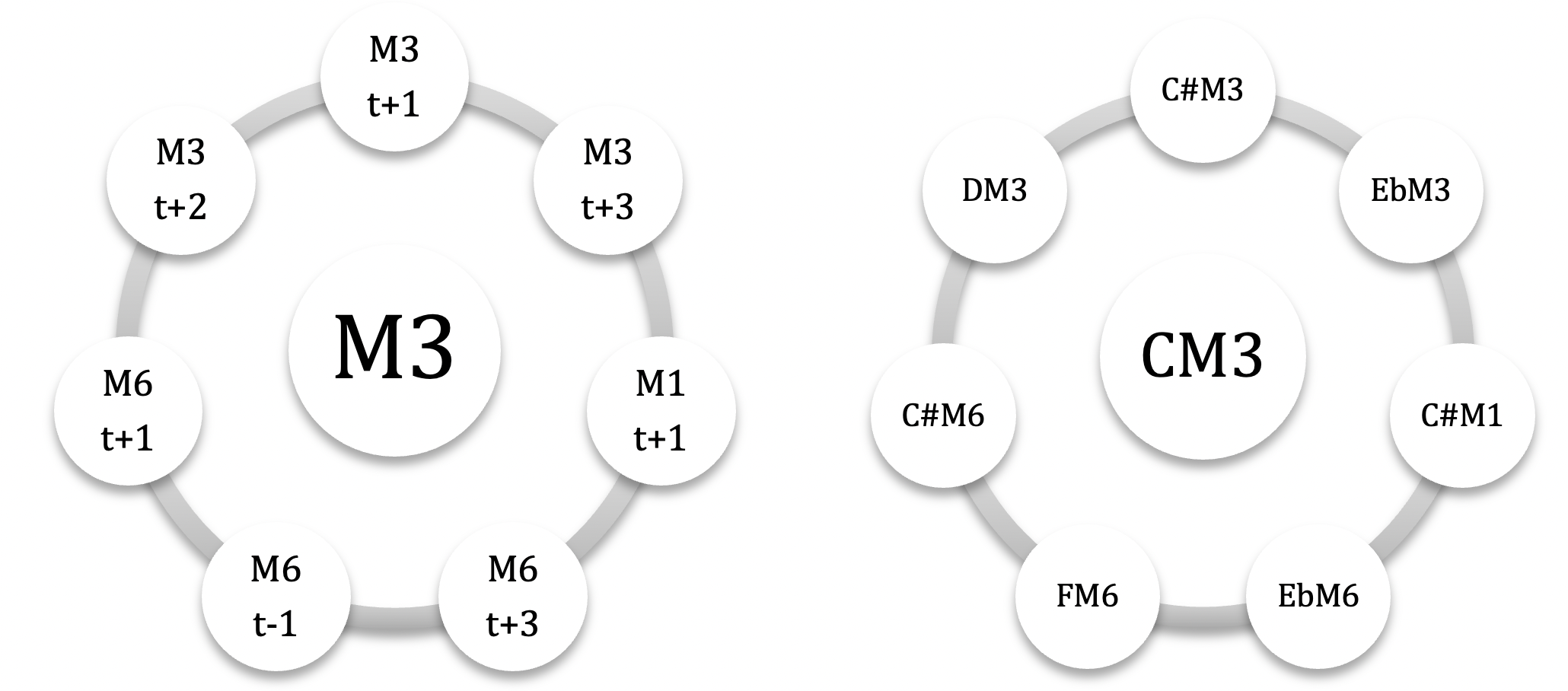
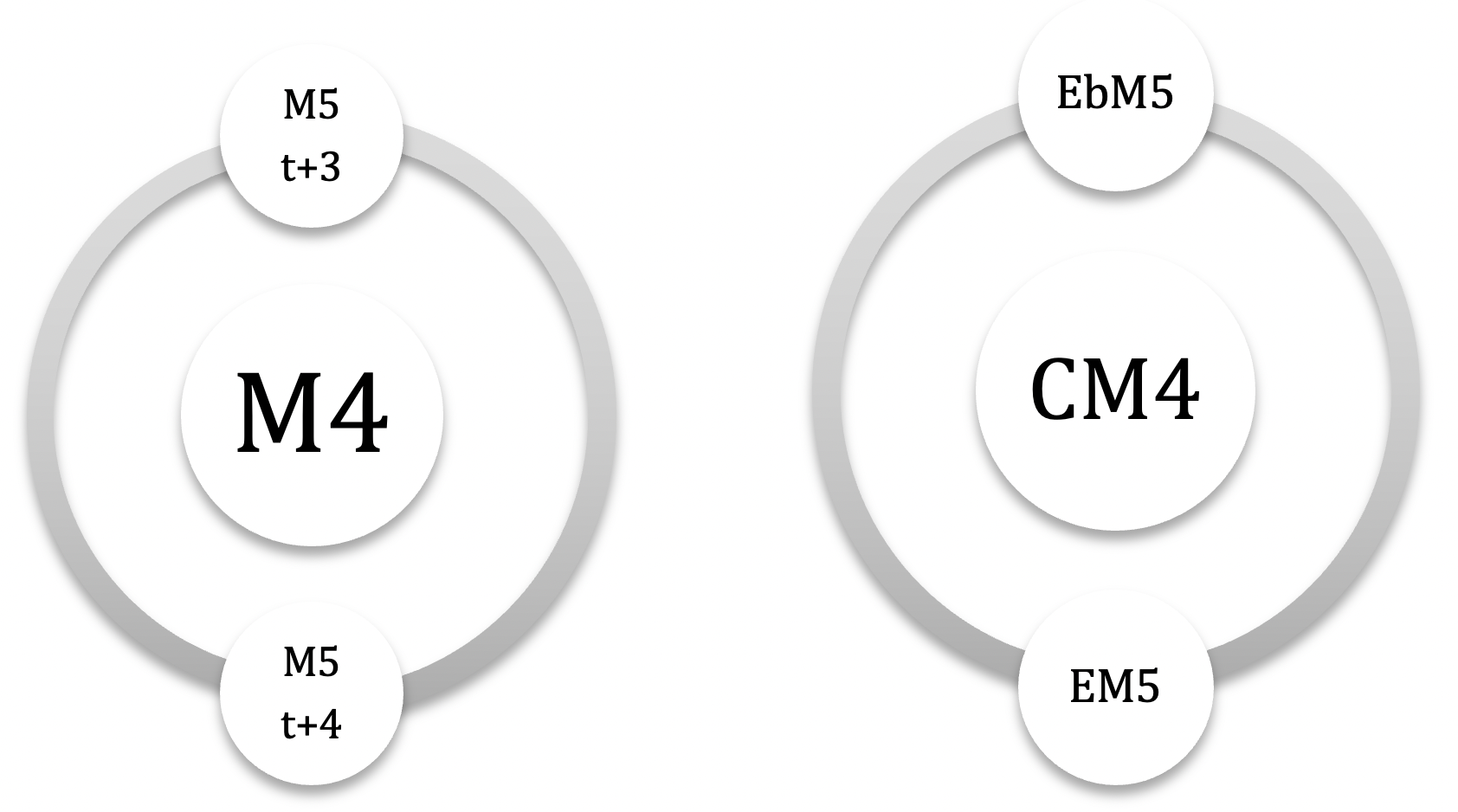
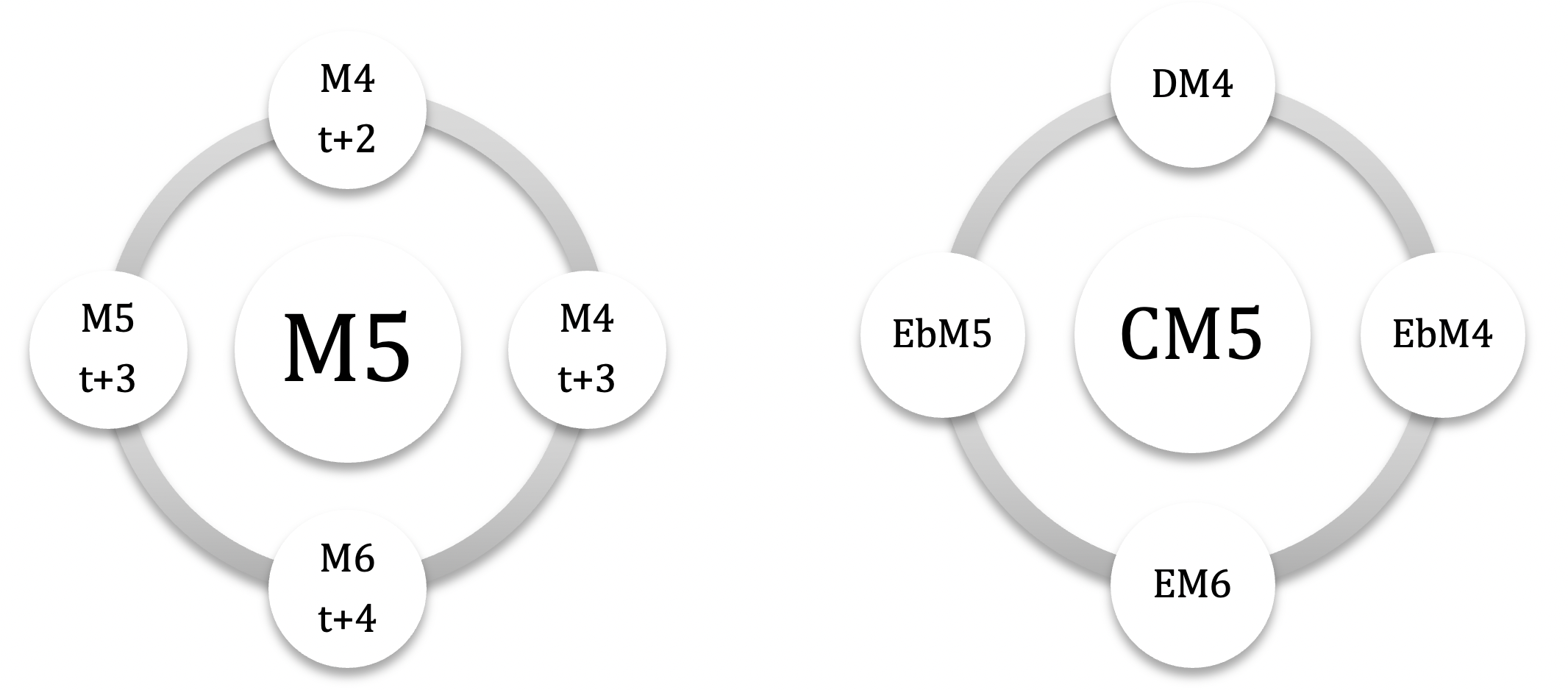
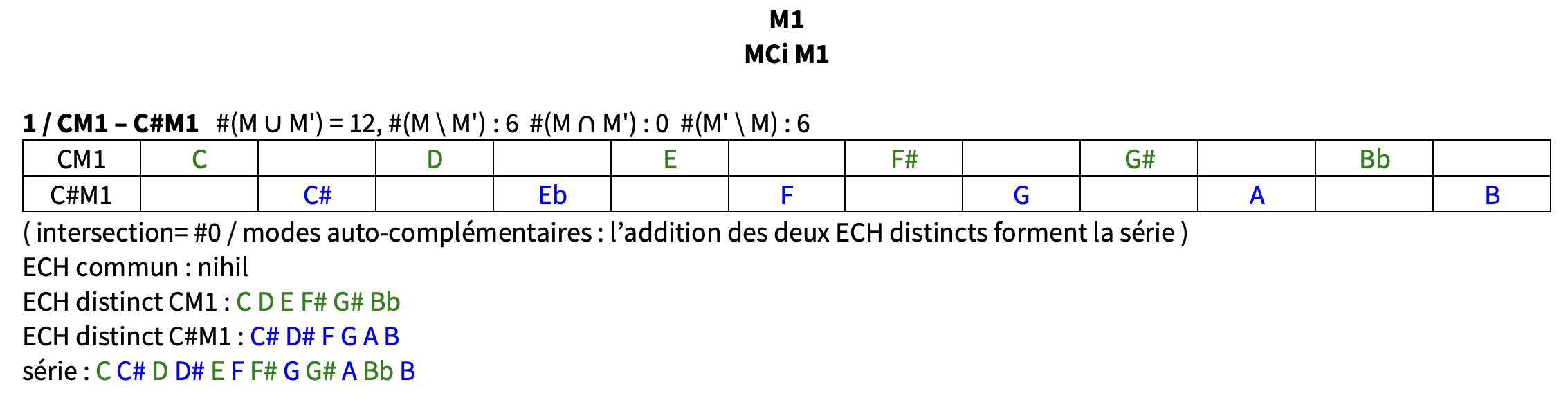
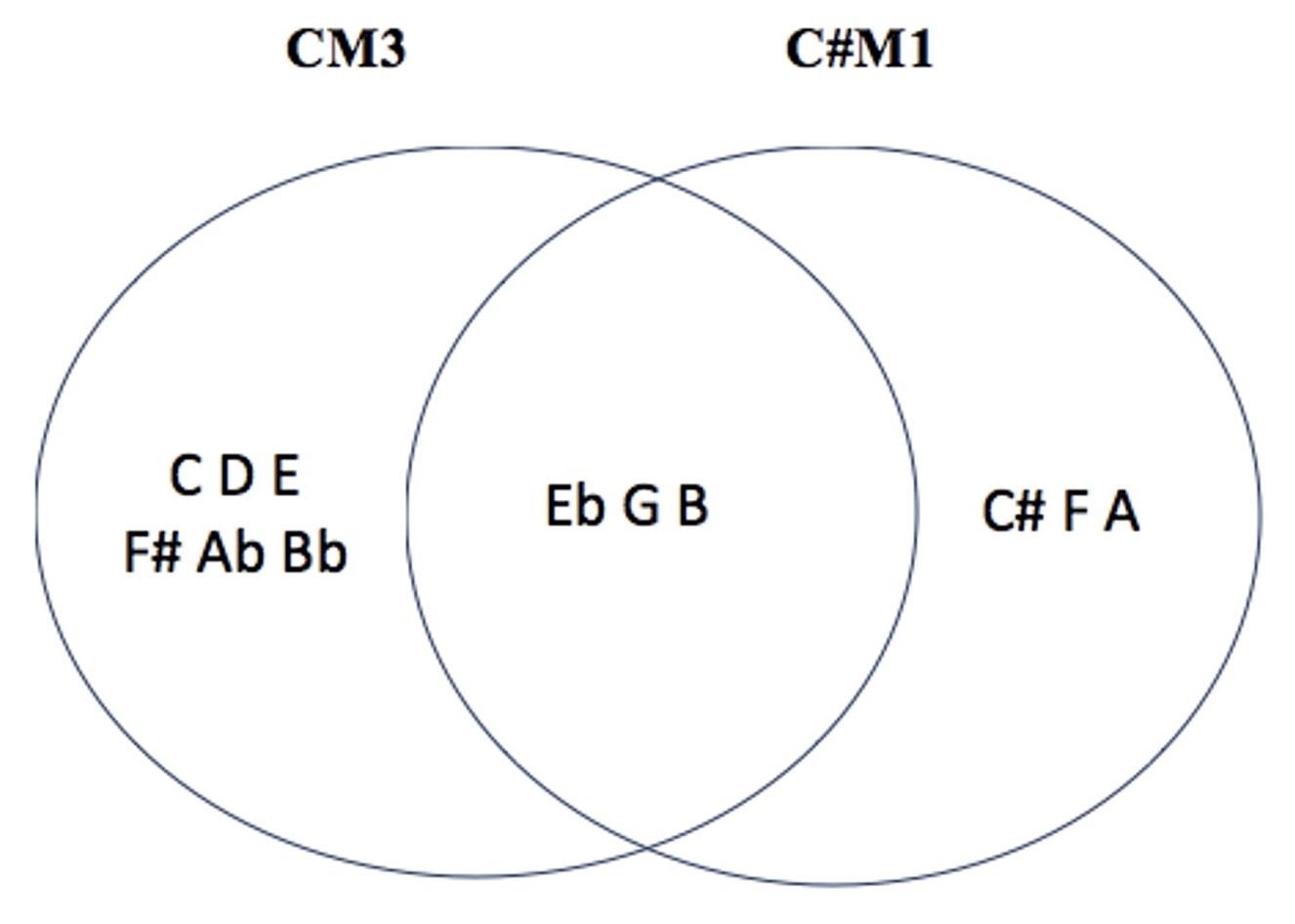
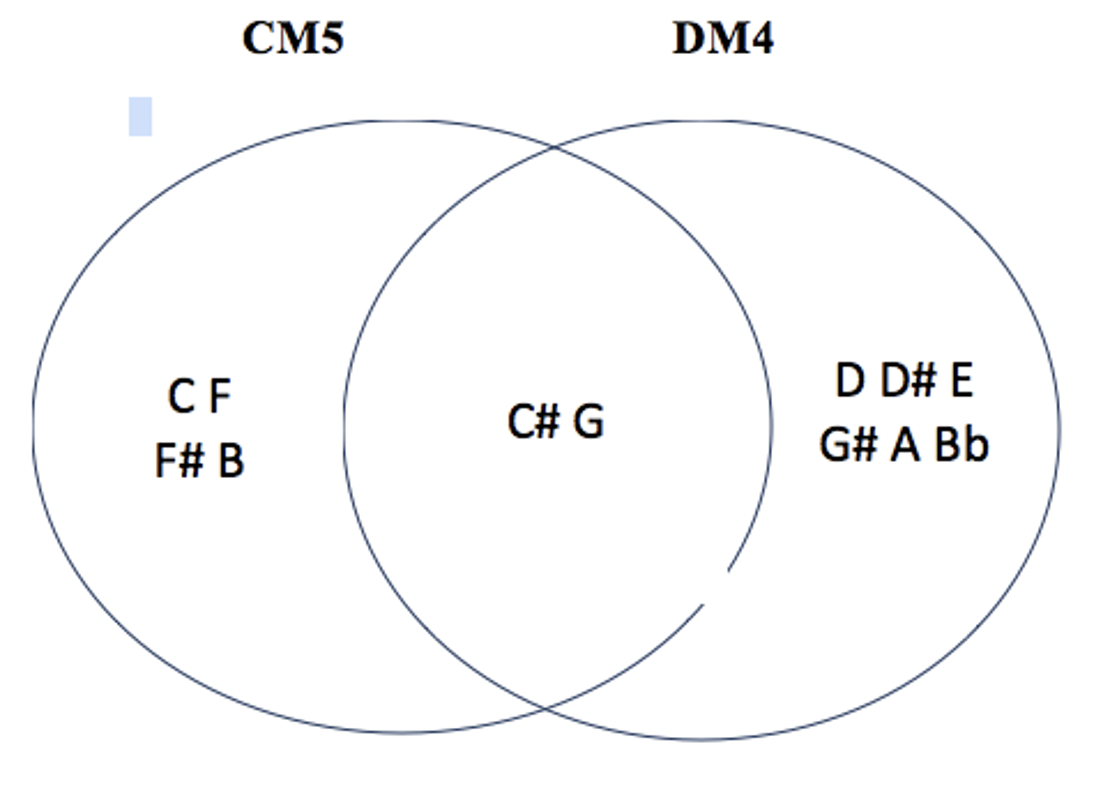
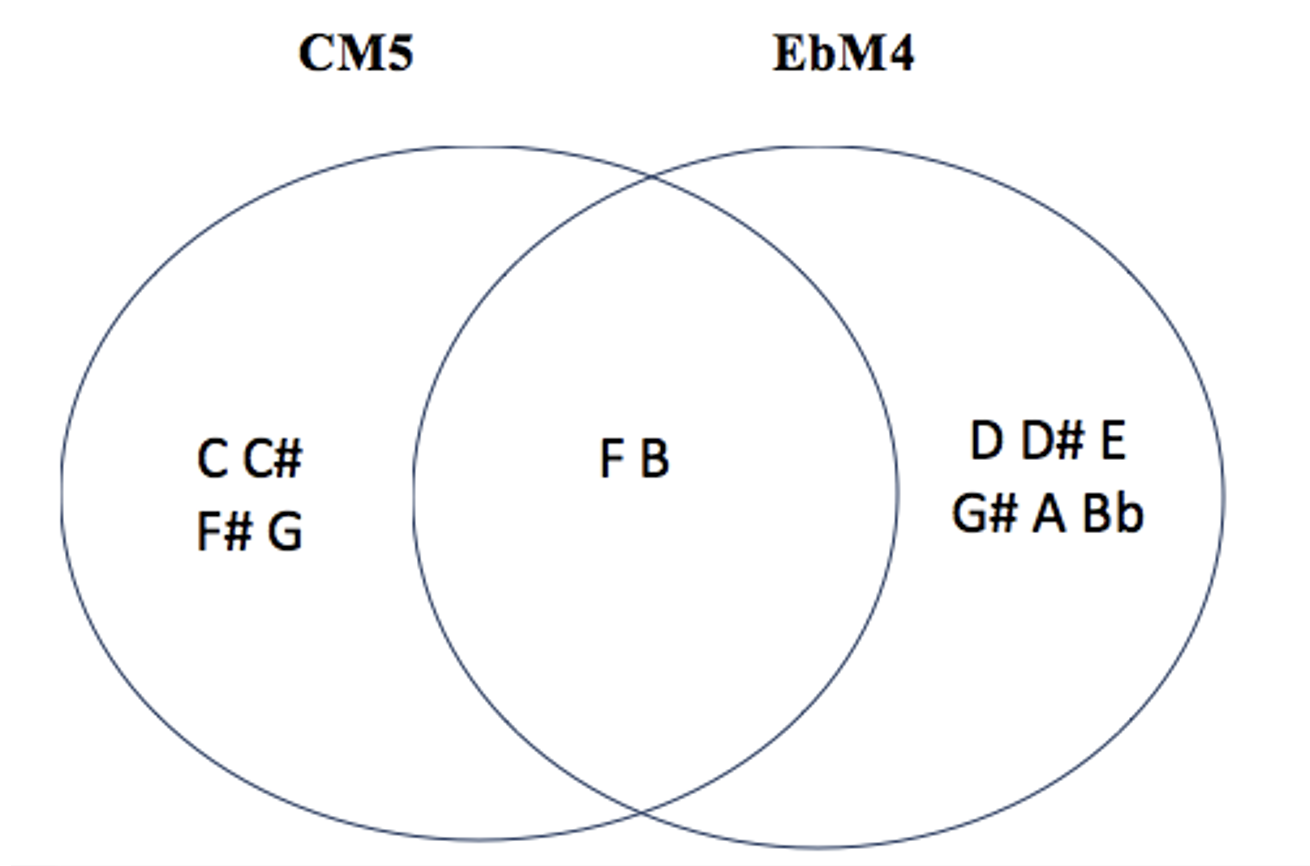
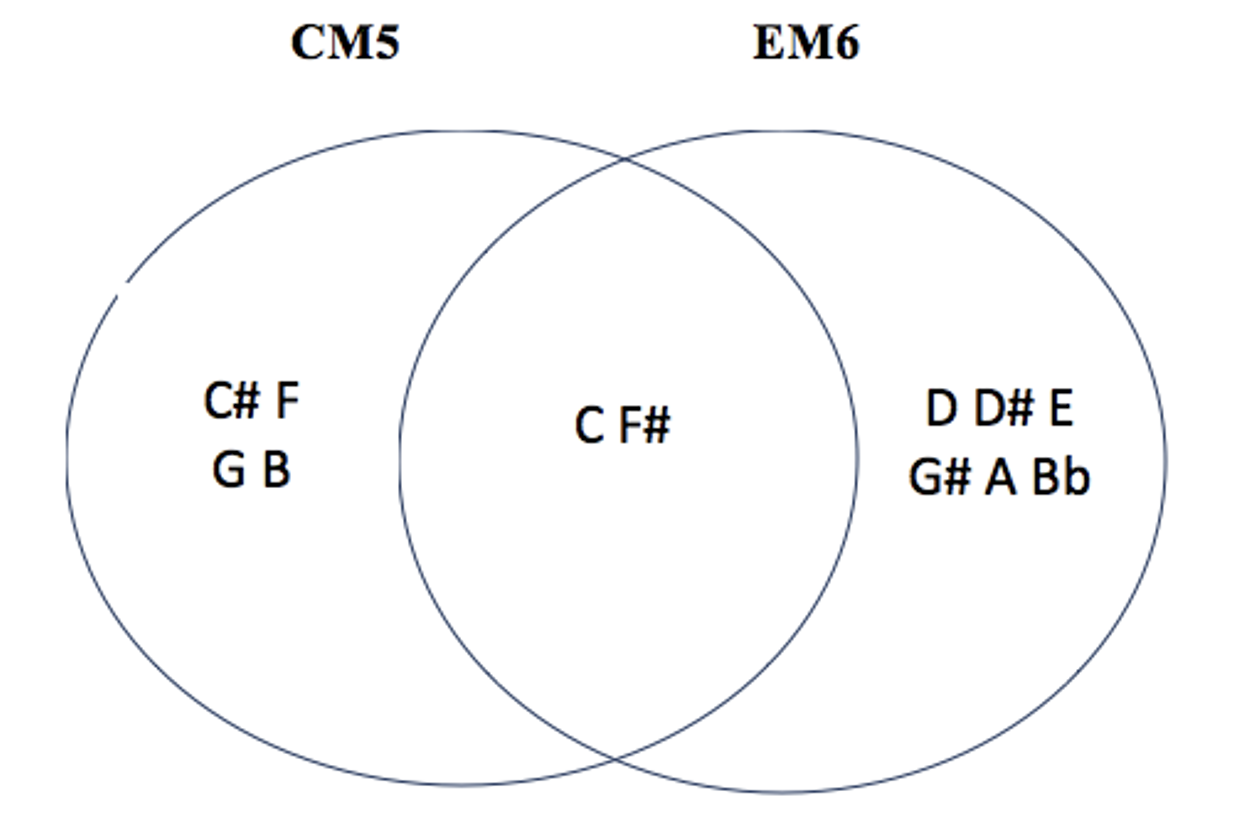
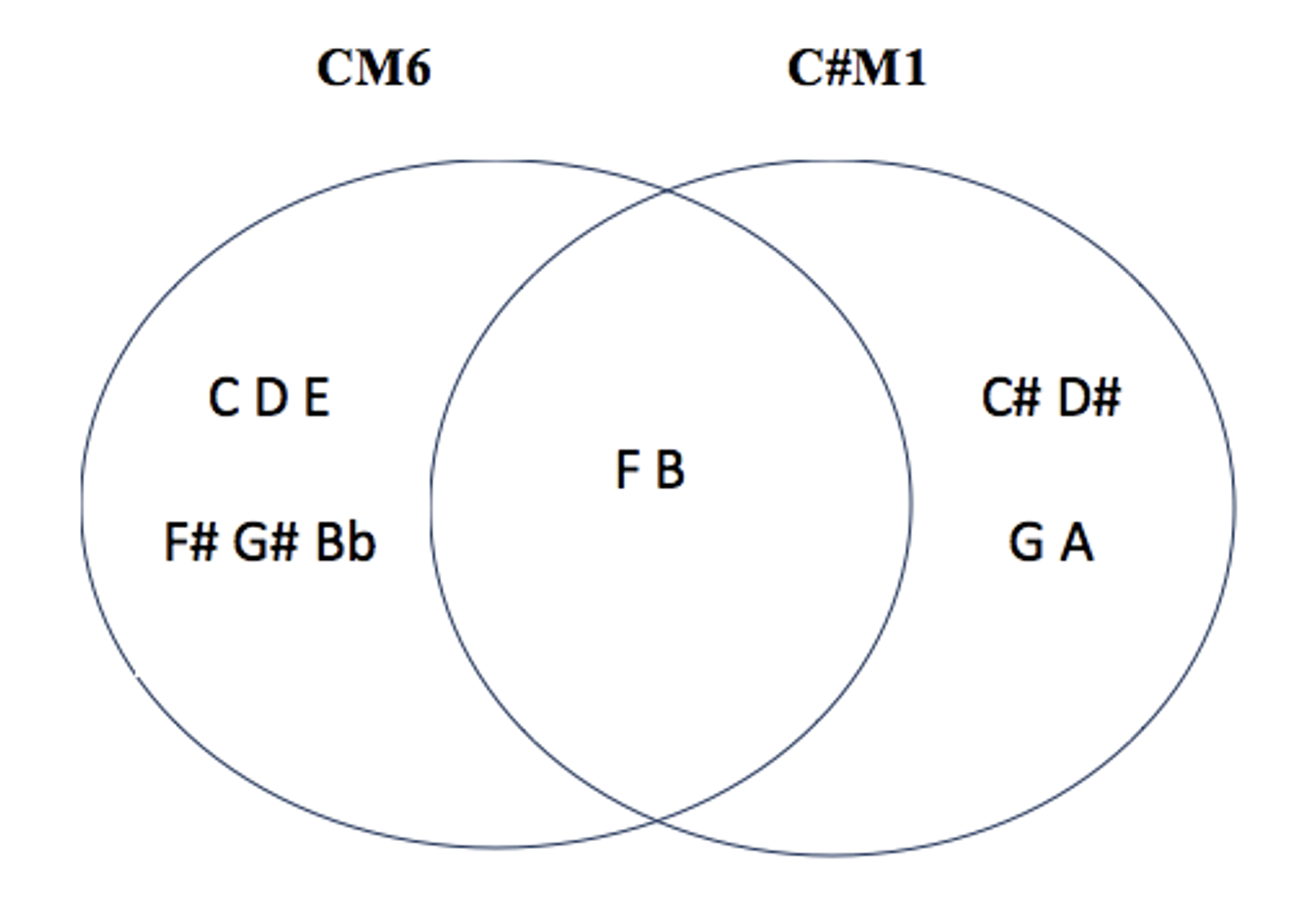
incluons les autres modes M1,M3 et M5 ( on exclut le mode 7 pour éviter une liste trop longue) / pour les différencier, les binômes seront nommés modes complémentaires irréguliers (MCi) car ils génèrent des champs souvent dissymétriques et hybrides, pouvant générer d’autres couleurs associées au mode nucleus / là où, pour les MC ‘réguliers’, la répartition modulo 12 était égale ( 3 x 4 : #(M \ M’)=4, #(M ∩ M’)=4 et (M’ \ M)=4 ), pour les MC irréguliers celle-ci sera hybride : intersections de 0, 2, 3, 5 ou 6 notes communes, en fonction des associations /pour M1, M3 et M5, les modes complémentaires sont tous Mci / pas de MCi pour M2 / 2 cas particuliers : CM1-C#M1 et CM5-EbM5, qui sont des modes auto-complémentaires: pas de notes communes et addition sérielle 6+6 )
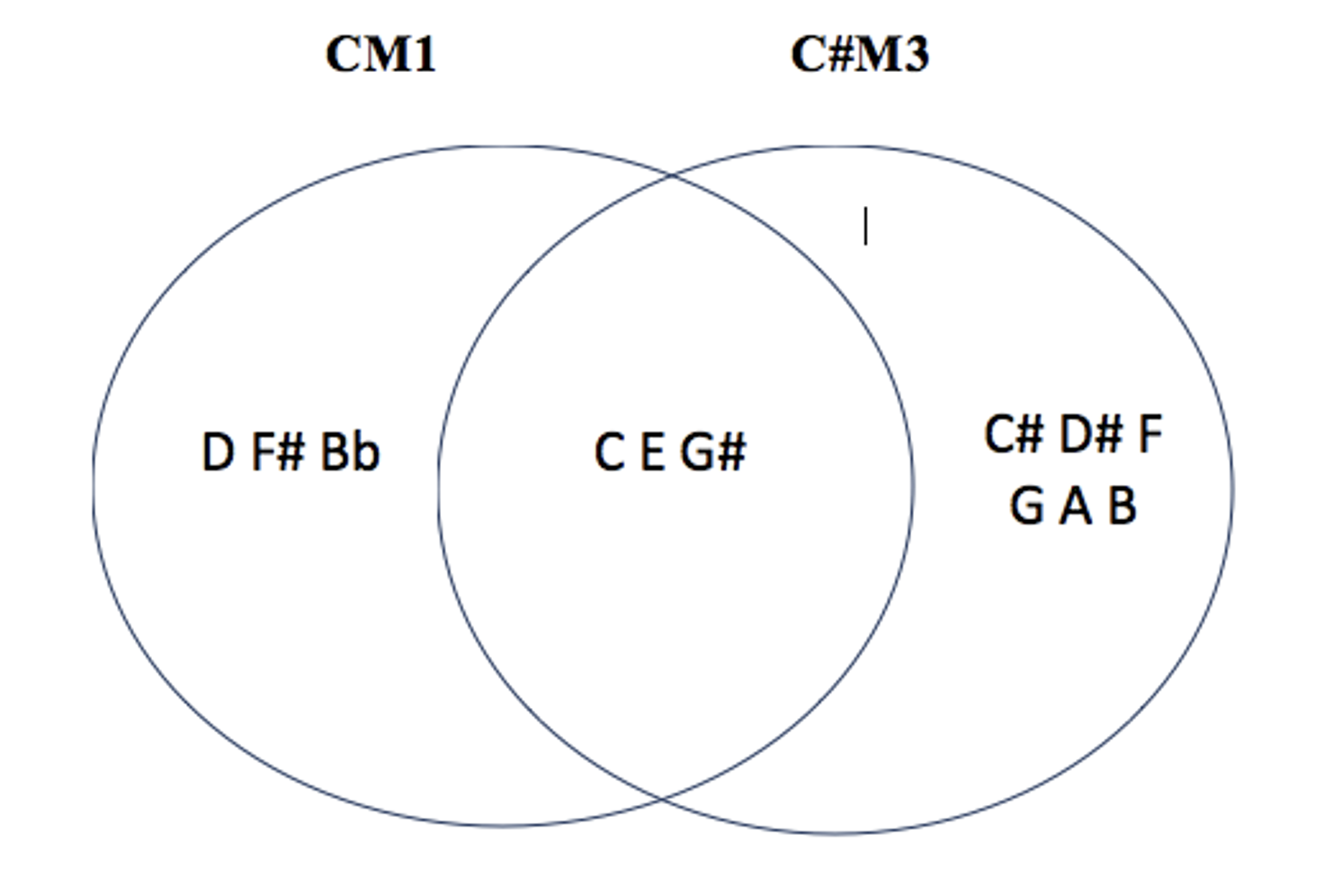
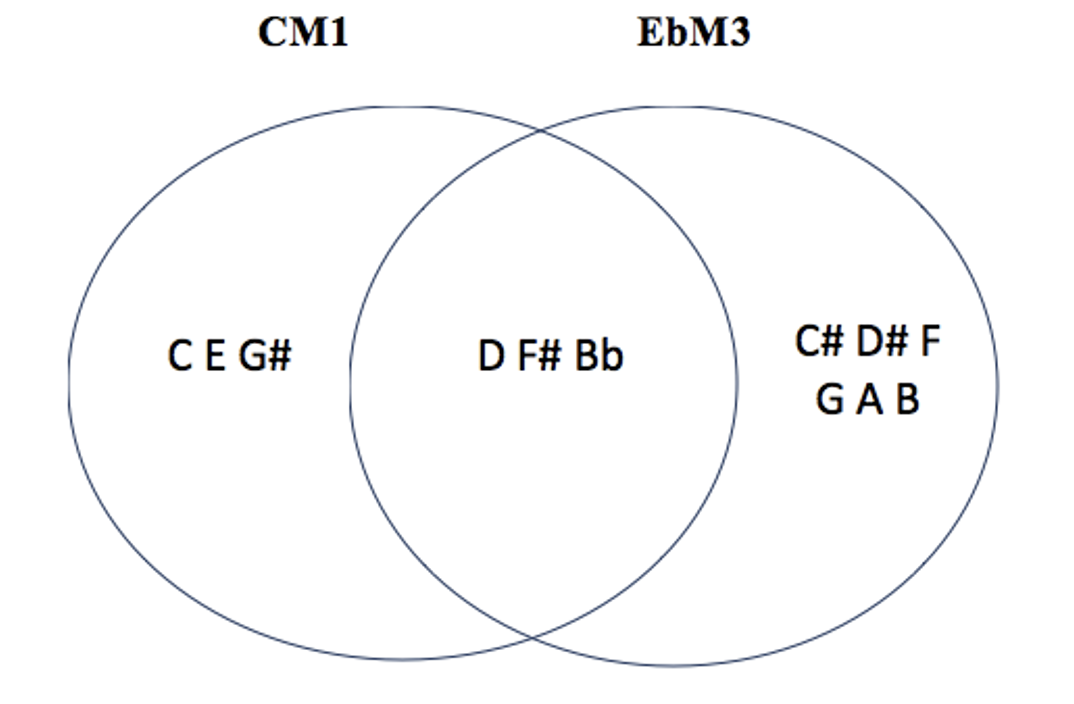
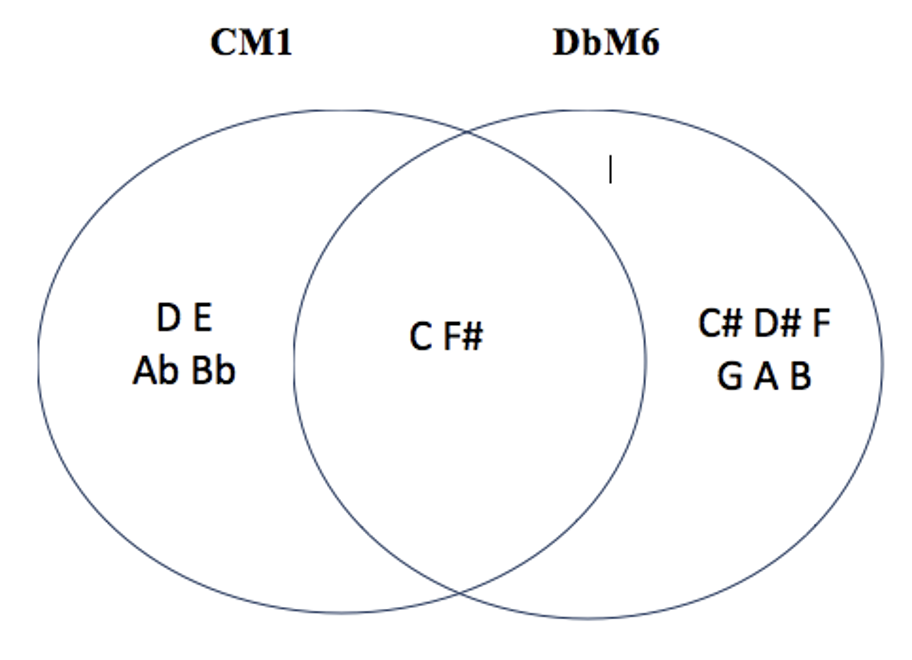
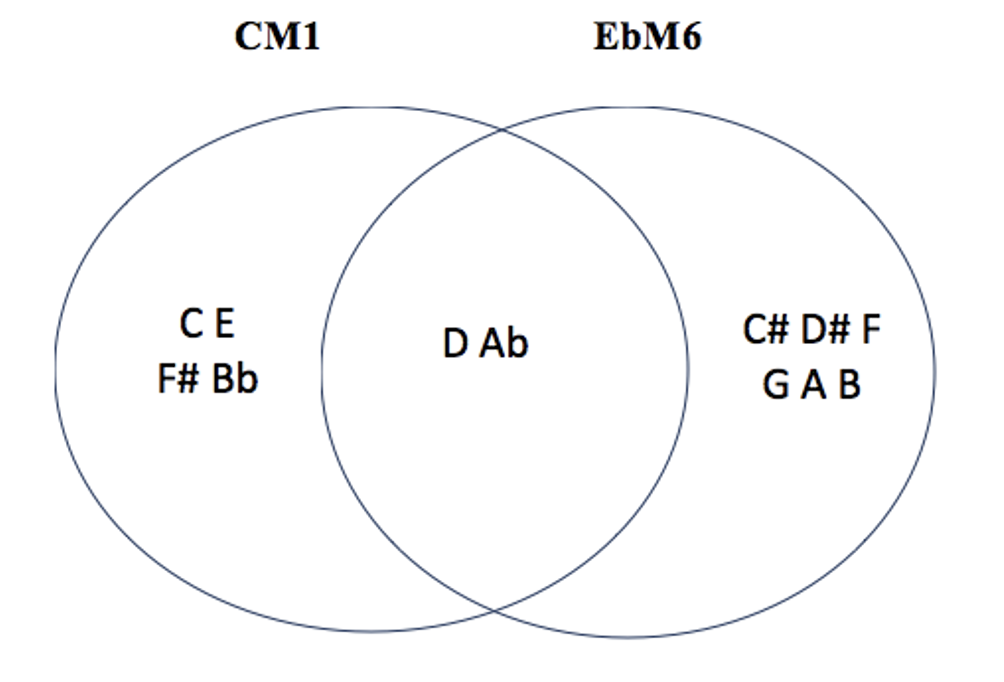
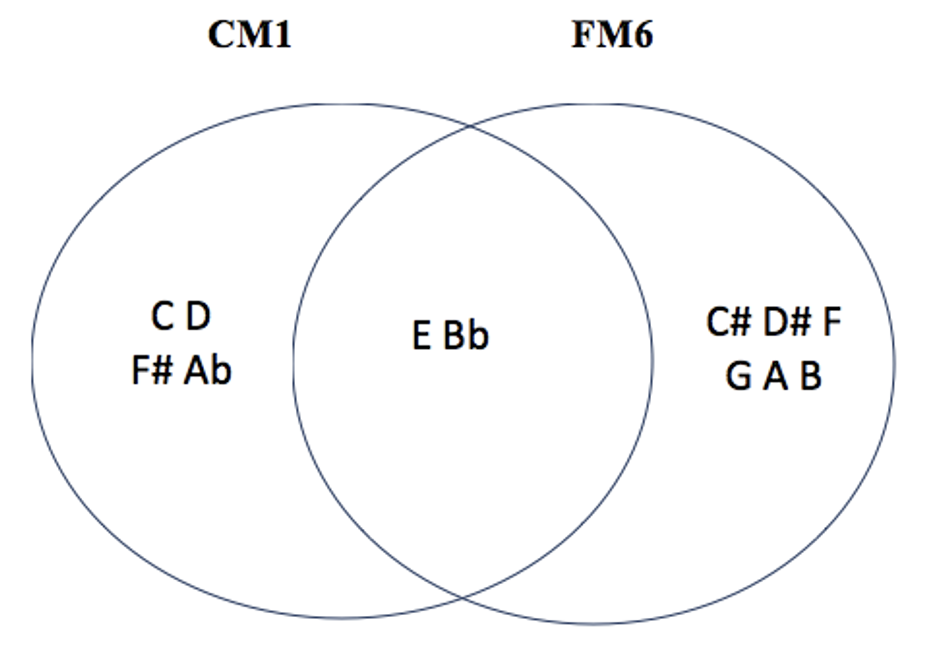
les 5 modes complémentaires irréguliers de CM1 : C#M3 – EbM3 – DbM6 – EbM6 – FM6
( + C#M1 : CM1 et C#M1 sont auto-complémentaires )
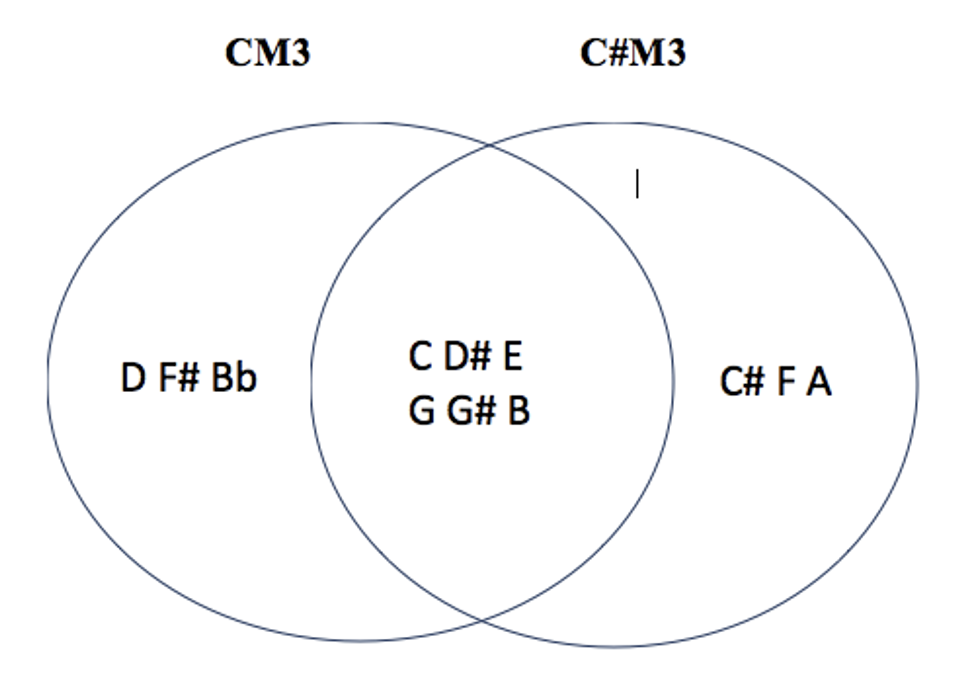
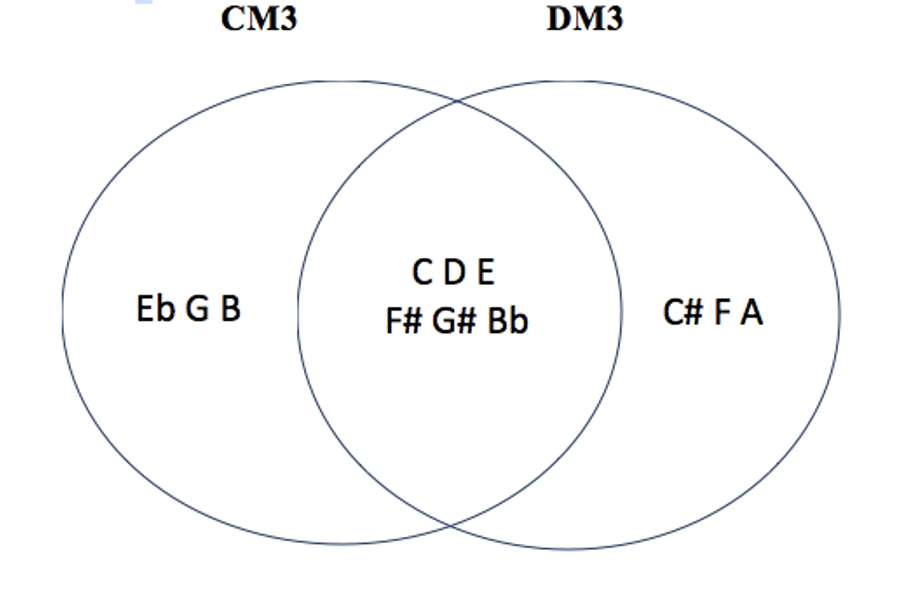
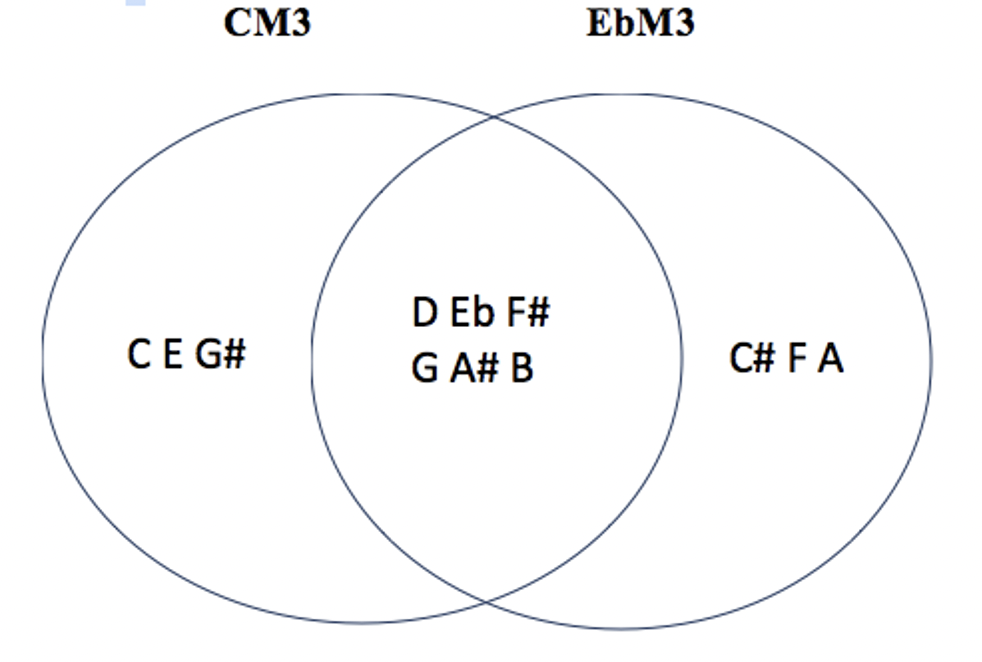
les 7 modes complémentaires irréguliers de CM3 : C#M1 – C#M3 – DM3 – EbM3 – C#M6 – EbM6 – FM6
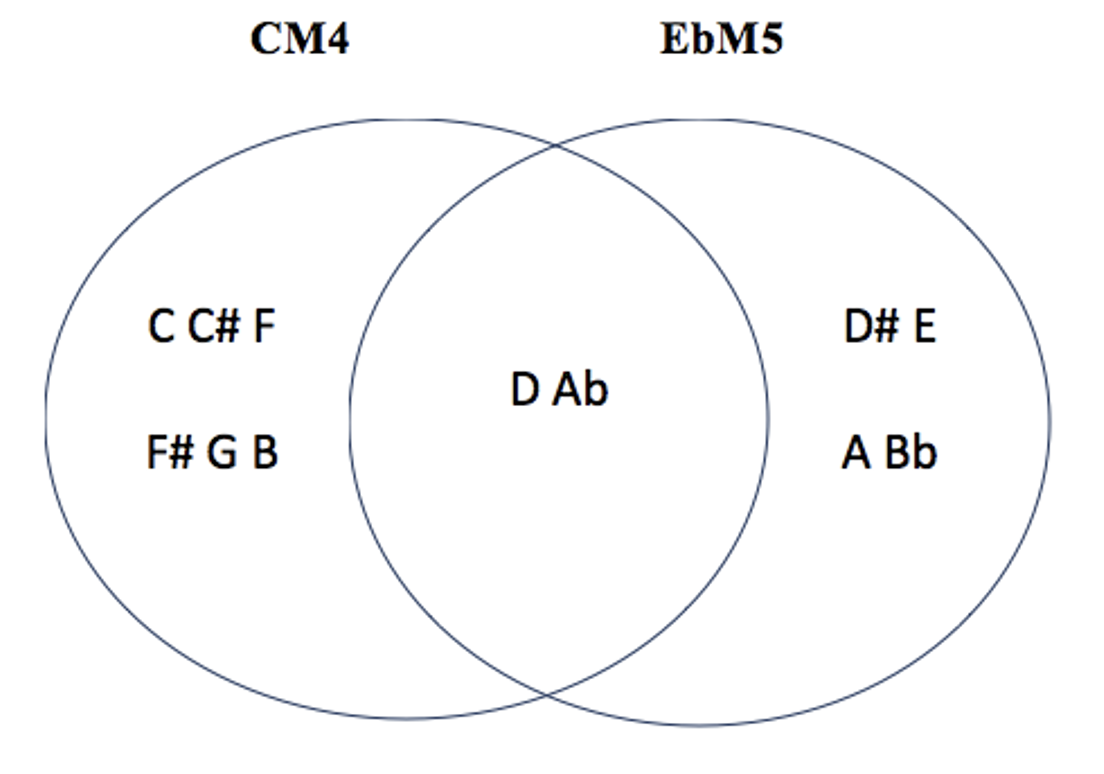
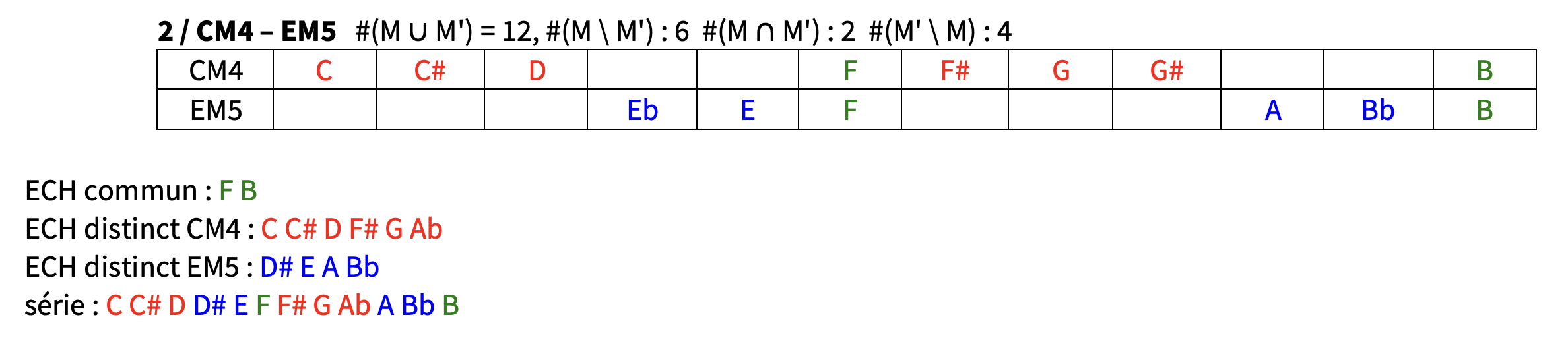
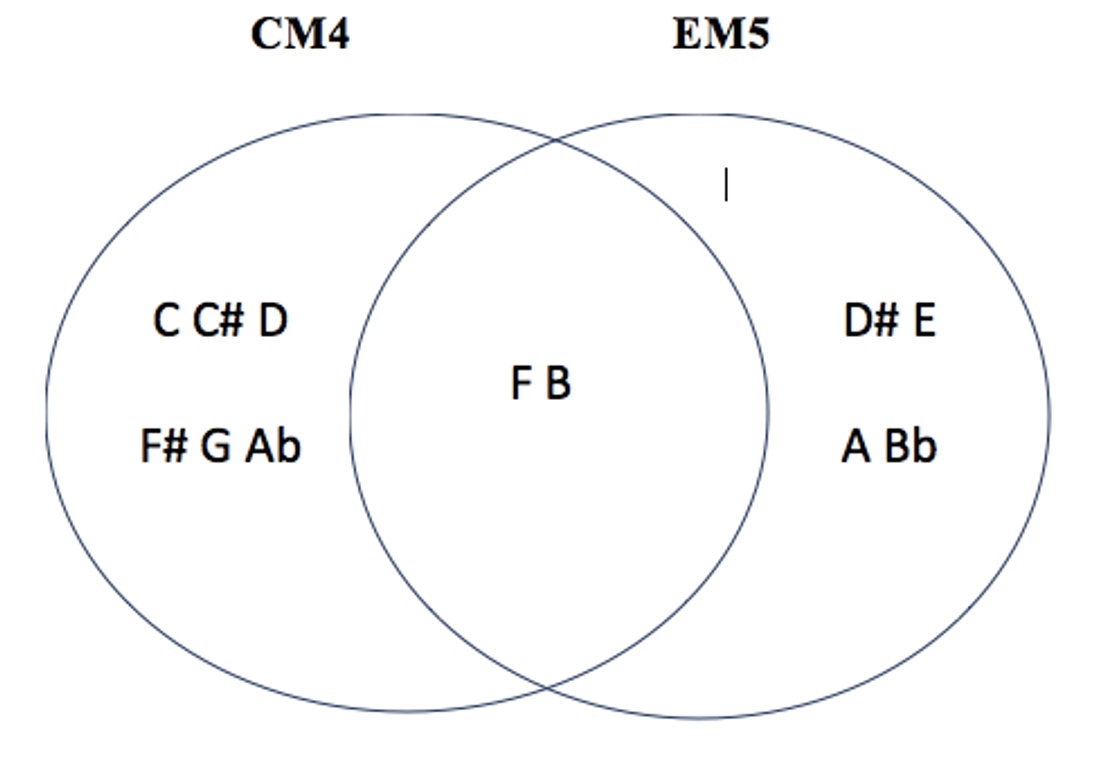
les 2 modes complémentaires irréguliers de CM4 : EbM5 – EM5
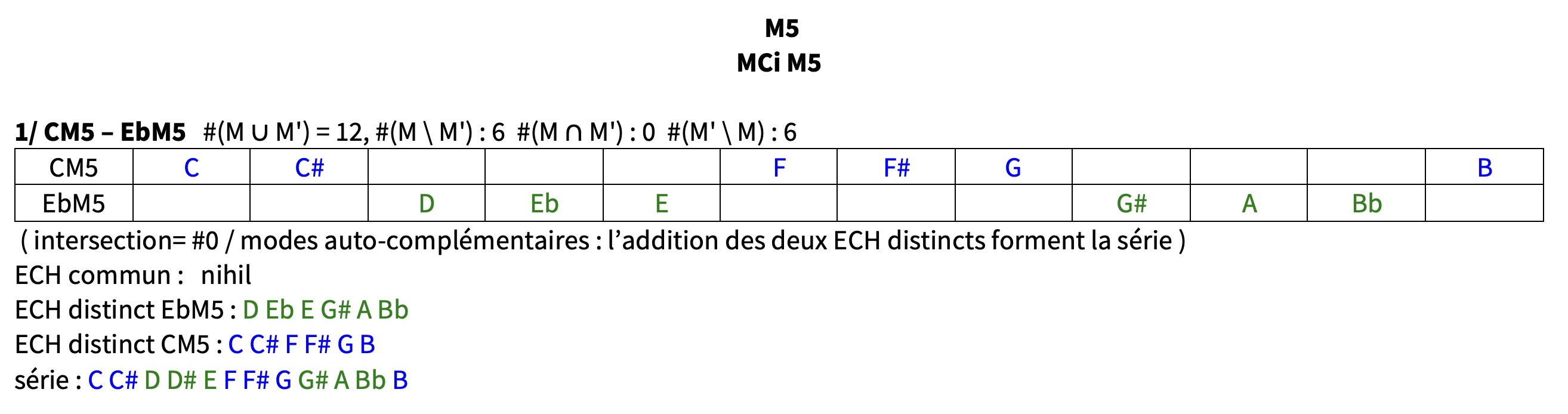
les 3 modes complémentaires irréguliers de CM5 : DM4 – EbM4 – EM6
( + EbM5 : CM5 et EbM5 sont auto-complémentaires )
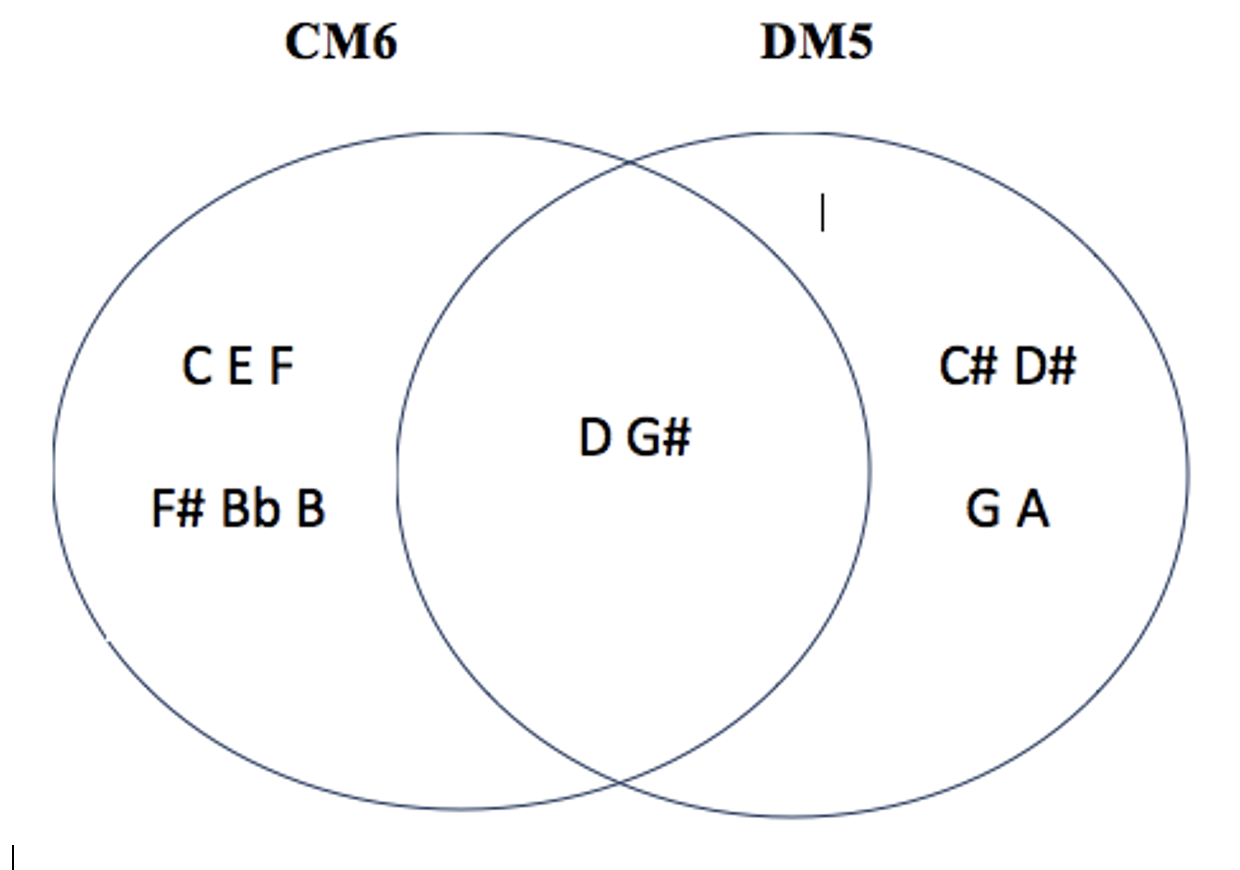
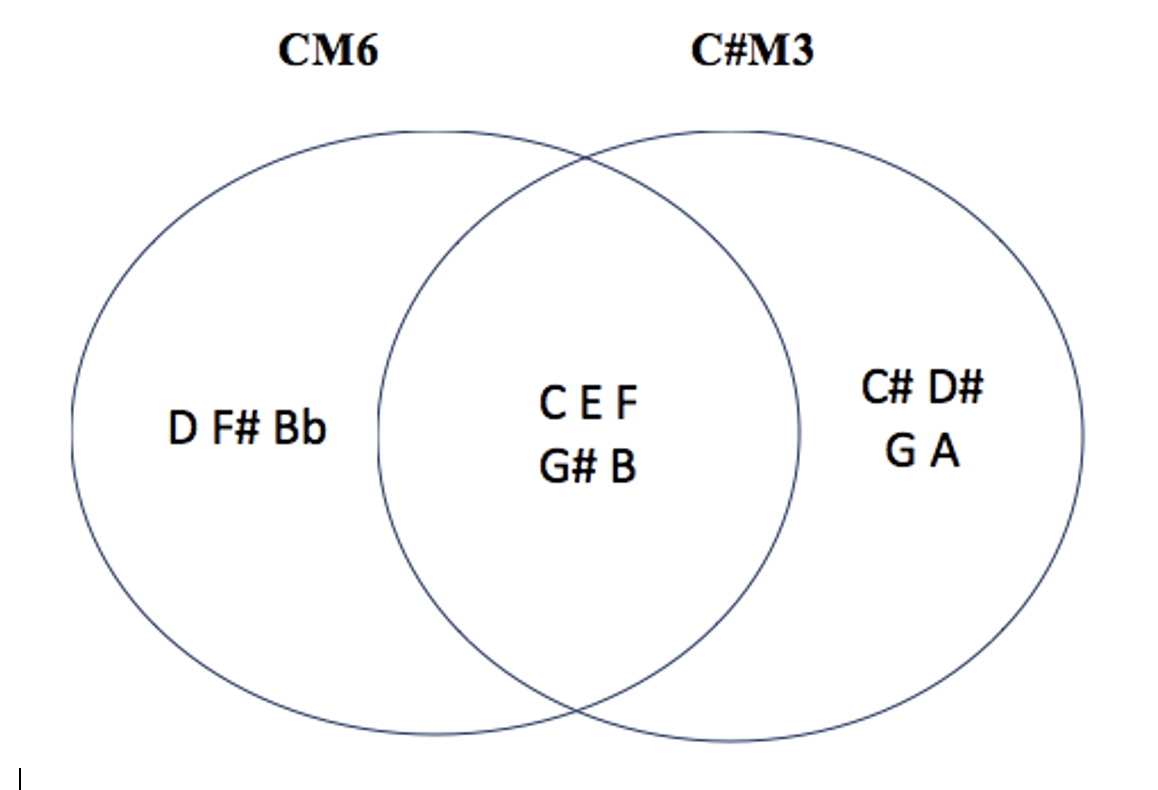
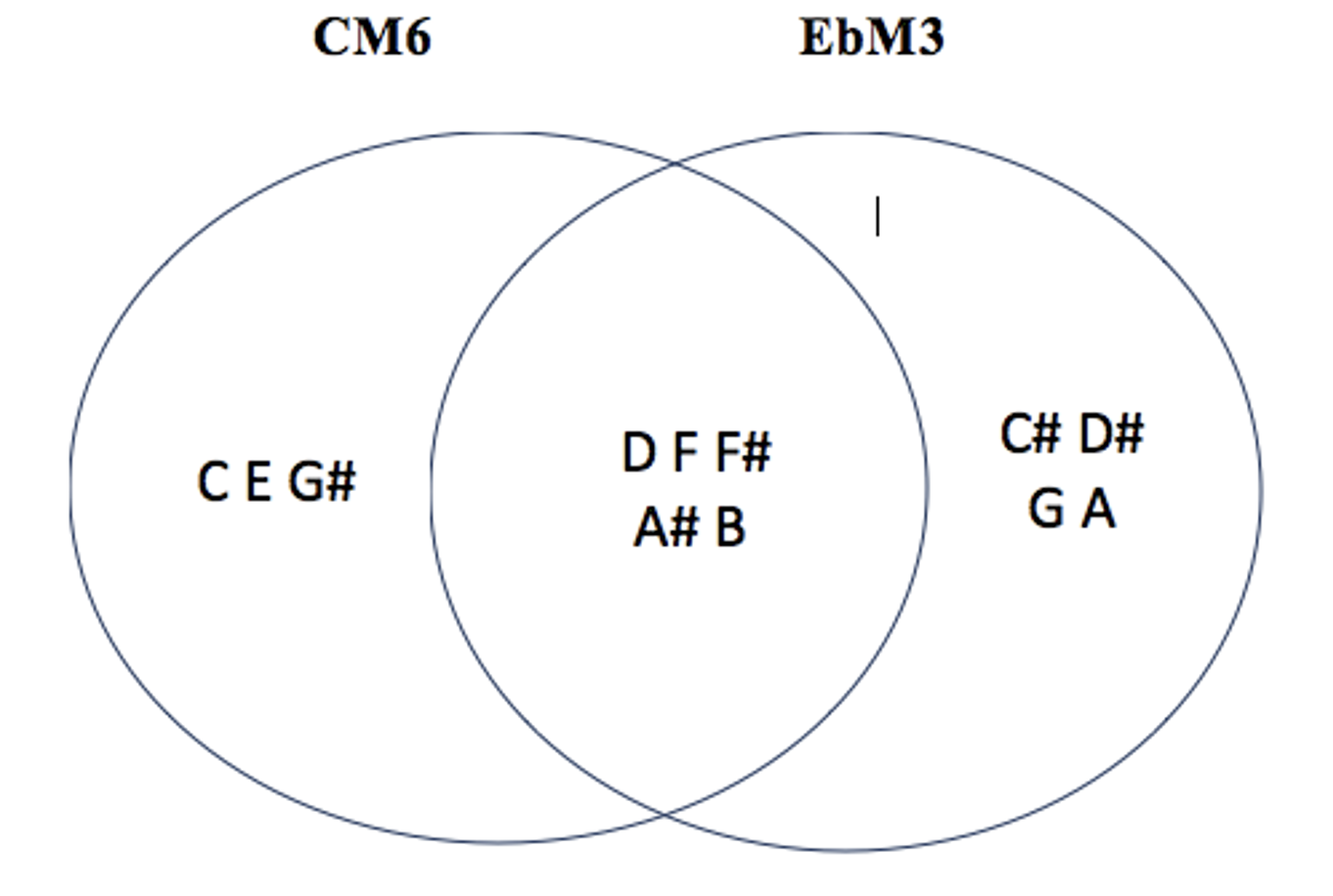
les 4 modes complémentaires irréguliers de CM6 : C#M1 – C#M3 – EbM3 – DM5