les modes à transpositions limitées : critères objectifs et subjectifs
‘ les modes sont des lieux colorés, des petits pays colorés…’( OM, conférence de KYOTO )
» les MATL n’ont pas de ton initial. Tout est transposition. Il n’y a ni tonique, ni initiale, ni finale. Les échelles mélodiques ne sont là que pour l’exposé. Les accords choisis ( ndla : ‘dans le traité’ ) sont frappants, mais on peut en faire beaucoup d’autres. Ces modes ne sont ni mélodiques, ni harmoniques : ce sont des couleurs ( en gras dans le texte original ) (…) Basés sur notre système chromatique actuel – système tempéré à 12 sons – ces modes sont formés de plusieurs groupes symétriques, la dernière note de chaque groupe étant toujours ‘commune’ avec la symétrie du groupe suivant. Au bout d’un certain nombre de transpositions chromatiques qui varie avec chaque mode, ils ne sont plus transposables – la 4ème transposition donnant exactement les mêmes notes que la 1ère par exemple, la 5ème donnant les mêmes que la 2ème…Ils sont trois. Plus 4 autres modes, six fois transposables, et présentant moins d’intérêt, en raison même de leur trop grand nombre de transpositions. Tous les MATL peuvent être utilisés mélodiquement- et surtout harmoniquement, mélodie et harmonie ne sortant jamais des notes du mode (…) Ils sont dans l’atmosphère de plusieurs tonalités à la fois, sans polytonalité – le compositeur étant libre de donner la prédominance à l’une des tonalités, ou de laisser l’impression tonale flottante. Leur série est close. Il est mathématiquement impossible d’en trouver d’autres » ( TLM, chapitre XVI )
critères objectifs
( le long procédé explicatif utilisé ici s’inspire librement du système de classification utilisé par DOMINIQUE RIVOLTA dans ‘genèse des échelles à transpositions limitées, et il est exhaustif / pour un raccourci, on peut faire défiler jusqu’à l’analyse chirurgicale des 7 modes
les modes à transpositions existent dans le système tempéré de l’échelle chromatique à douze demi-tons
1/ division de l’octave en 12 parts égales
= la gamme chromatique, ensemble non transposable.
2/ division de l’octave en 6 parts égales
on obtient la gamme par tons, c’est le premier mode à transpositions limitées :
2 transpositions possibles: CM1 ( C D E F# G# Bb ) et DbM1 ( Db Eb F G A B )
(nommés M1 1 et M1 2 dans la terminologie de OM)
CM1 = DM1 = EM1 = F#M1 = AbM1 = BbM1
C#M1 = EbM1 = FM1 = GM1 = AM1 = BM1
3/ division de l’octave en 4 parts égales
a) on obtient l’accord diminué, dont il existe 3 transpositions : C Eb F# A / C# E G Bb / D F Ab B ( cf 5d )
b) en combinant deux accords diminués, on obtient une échelle octatonique, c’est le deuxième mode à transpositions limitées ( nommée ‘gamme diminuée’ ou gamme ‘octatonique’ en jazz : demi-ton/ton ou ton/demi-ton )
il existe 3 transpositions:
CM2 ( C C# D# E F# G A Bb )
C#M2 ( C# D E F G Ab Bb B )
DM2 ( D Eb F F# G# A B C )
CM2 = EbM2 = F#M2 = AM2
C#M2 = EM2 = GM2 = BbM2
DM2 = FM2 = AbM2 = BM2
nb: chaque note de M2 fait partie d’un accord diminué
on se référera entre autres à ‘TLM’ ( ex 312 à 328 ) pour quelques exemples musicaux utilisant le second mode à transpositions limitées
4/ division de l’octave en 3 parts égales
a) on obtient l’accord augmenté (l’accord augmenté se retrouve dans M1, M3, M6 et M7)
il existe 4 transpositions:
C E G#
Db F A
D F# A#
Eb G B
b) en ajoutant un demi-ton inférieur (ou supérieur) à chacune des trois notes de l’accord augmenté, on obtient une échelle hexatonique
( souvent appelée ‘gamme augmentée’ en jazz )
il existe 4 transpositions:
(B)C D#E G G# B(C)
(C)Db EF G#A C(Db)
(C#)D FF# ABb C#(D)
(D)Eb F#G A#B D(Eb)
c) en ajoutant un demi-ton inférieur et supérieur à chacune des trois notes, on obtient une échelle ennéatonique,
c’est le troisième mode à transpositions limitées, il existe 4 transpositions:
CM3 = C D Eb E F# G G# A# B ( M3 1 )
C#M3 = C# D# E F G Ab A B C ( M3 2 )
DM3 = D E F F# G# A Bb C Db ( M3 3 )
EbM3 = Eb F Gb G A Bb B C# D ( M3 4 )
CM3 = EM3 = G#M3 / C#M3 = FM3 = AM3 / DM3 = F#M3 = BbM3 / EbM3 = GM3 = BM3
nb: M3 est le seul mode à transpositions limitées qui divise l’octave en 3 parties symétriques
nb: chaque note de M3 fait partie d’une triade augmentée
on se référera entre autres à TLM ( ex 329 à 340 ) pour quelques exemples musicaux choisis par OM pour illustrer le troisième MATL
5/ division de l’octave en 2 parts égales
a) on obtient l’intervalle de quarte augmentée, six transpositions possibles: C-F# / C#-G / D-G# / Eb-A / E-Bb / F-B
b) en ajoutant un demi-ton inférieur (ou supérieur) à chacune des deux notes, on obtient un accord hybride à 4 notes transposable 6x :
(B)C (F)F#
(C)C# (F#)G
(C#)D (G)Ab
(D)Eb (G#)A
(D#)E (A)Bb
(E)F (A#)B
c) en ajoutant un demi-ton inférieur et un demi-ton supérieur (*) à chacune des deux notes de 5a on obtient une échelle hexatonique transposable 6x, c’est le 5ème mode à transpositions limitées :
CM5 = (B)C(C#) (F)F#(G)
C#M5 = (C)C#(D) (F#)G(Ab)
DM5 = (C#)D(Eb) (G)Ab(A)
EbM5 = (D)Eb(E) (G#)A(Bb)
EM5 = (D#)E(F) (A)Bb(B)
FM5 = (E)F(F#) (A#)B(C)
nb: comme pour tous les autres modes transposables 6x, chaque note de M5 a son ‘équivalent triton’
d) en ajoutant une tierce mineure à chacune des deux notes de 5a, on obtient un accord diminué, transposable 3 fois ( cf 3a )
C (Eb) F# (A) ( = Eb F# A C ) = C°7/Eb°7/F#°7/A°7
C# (E) G (Bb) ( = E G Bb C# ) = C#°7/E°7/G°7/Bb°7
D (F) B (Cb) ( = F Ab B D ) = D°7/F°7/Ab°7/B°7
e) en ajoutant un tierce majeure à chacune des deux notes de 5a, on obtient un accord dominant b5, transposable 6x :
C (E) F# (Bb) = C7b5/F#7b5
C# (F) G (B) = C#7b5/G7b5
D (F#) Ab (C) = D7b5/Ab7b5
Eb (G) A (Db) = Eb7b5/A7b5
E (G#) Bb (D) = E7b5/Bb7b5
F (A) B (Eb) = F7b5/B7b5
f) en ajoutant une seconde majeure et une quarte juste à chacune des deux notes de 5a, on obtient un échelle hexatonique ( incluse dans le deuxième mode à transpositions limitées. C’est, dans la terminologie de MESSIAEN, un mode 2 tronqué )
C(D F)F#(G# B) = troncation de DM2 ( manquent Eb et A pour former DM2 )
C#(D# F#)G(A C) = troncation de CM2
D(E G)Ab(Bb Db) = troncation de C#M2
Eb(F Ab)A(B D) = troncation de DM2
E(F#A)Bb(CEb) = troncation de CM2
F(G Bb)B(C#E) = troncation de C#M2
g) en ajoutant une tierce mineure et une quarte juste à chacune des deux notes de 5a, on obtient un échelle hexatonique ( également incluse dans le deuxième mode à transpositions limitées = mode 2 tronqué )
C(Eb F)F#(A B) = troncation de DM2 ( manquent D et Ab pour former DM2 )
C#(E F#)G(Bb C) = troncation de CM2
D(F G)G#( B C#) = troncation de C#M2
Eb(Gb Ab)A(C D) = troncation de DM2
E(G A)Bb(Db Eb) = troncation de CM2
F(Ab Bb)B(D E) = troncation de C#M2
h) en ajoutant une seconde majeure inférieure et supérieure à chacune des deux notes de 5a, on obtient le premier mode à transpositions limitées (cf 2)
C(D E)F#(G# Bb) = CM1
C#(D# F)G(A B) = C#M1
D(E F#)Ab(Bb C) = CM1
Eb(F G)A(B C#) = C#M1
E(F#G#)Bb(CD) = CM1
F(G A)B(C#D#) = C#M1
i) en ajoutant une seconde mineure inférieure et deux secondes mineures supérieures (*) à chacune des deux notes de 5a,
on obtient le quatrième mode à transpositions limitées, transposable 6x :
CM4 = (B)C(C# D) (F)F#(G Ab)
C#M4 = (C)C#(D Eb) (F#)G(Ab A)
DM4 = (C#)D(Eb E) (G)Ab(A Bb)
EbM4 = (D)Eb(E F) (G#)A(Bb B)
EM4 = (D#)E(F F#) (A)Bb(B C)
FM4 = (E)F(F# G) (A#)B(C C#)
nb: comme pour tous les autres modes transposables 6x, chaque note de M4 a son ‘équivalent triton’
on se référera entre autres à ‘TLM’ ( ex 345 et 346 ) pour quelques exemples musicaux choisis par Messiaen pour illustrer le quatrième mode à transpositions limitées.
j) en rajoutant une seconde mineure inférieure et deux secondes majeures supérieures (*) à chacune des deux notes de 5a,
on obtient le sixième mode à transpositions limitées, transposable 6x :
CM6 = F#M6 = (B)C(D E) (F)F#(G# A#)
C#M6 = GM6 = (C)Db(Eb F) (F#)G(A B)
DM6 = AbM6 = (C#)D(E F#) (G)Ab(Bb C)
EbM6 = AM6 = (D)Eb(F G) (G#)A(B C#)
EM6 = BbM6 = (D#)E(F# G#) (A)Bb(C D)
FM6 = BM6 = (E)F(G A) (A#)B(C# D#)
nb: comme pour tous les autres modes transposables 6x, chaque note de M6 a son ‘équivalent triton’
on se référera entre autres à ‘TLM’ ( ex 350 à 353 ) pour quelques exemples musicaux choisis par MESSIAEN pour illustrer le sixième mode à transpositions limitées.
k) dernière combinaison possible, en rajoutant toutes les notes manquantes excepté la tierce majeure de chacune des deux notes de 5a ( ou vu autrement, l’échelle chromatique excepté l’intervalle 5a), on obtient une échelle décaphonique,
c’est le 7ème mode à transpositions limitées , transposable 6x :
C(D Eb F)F#(G G# A B) = CM7 = F#M7
C#(D Eb E F#)G(G# A Bb C) = C#M7 = GM7
D(Eb E F G)G#(A Bb B C#) = DM7 = AbM7
Eb(E F F# G#)A(Bb B C D) = EbM7 = AM7
E(F F# G A)Bb(B C Db Eb) = EM7 = BbM7
F(F# G Ab Bb)B(C C# D E) = FM7 = BM7
nb: comme pour tous les autres modes transposables 6x, chaque note de M7 a son ‘équivalent triton’
on se référera entre autres à ‘TLM’ ( ex 354 à 357 ) pour quelques exemples musicaux choisis par Messiaen pour illustrer le septième mode à transpositions limitées.
au total : 15 ensembles à transpositions limitées, incluant les 7 modes sélectionnés par Messiaen
en ordre croissant:
1) – ensemble de 2 sons ( transposable 6x ) : 5a ( C41 / F#41 )
2) – ensemble de 3 sons ( transposable 4x ) : 4a ( C111 / E111 / G#111 )
3) – ensemble de 4 sons ( transposable 3x ) : 3a / 5d ( C249 / Eb249 / F#249 / A249 )
4) – ensemble de 4 sons ( transposable 6x ) : 5b ( Cc3 / F#c3 )
5) – ensemble de 4 sons ( transposable 6x ) : 5 e ( C145 / F#145 )
6) – ensemble de 6 sons ( transposable 2x ) : M1: 2 ( CM1 / DM1 / EM1 / F#M1 / G#M1 / BbM1 )
7) – ensemble de 6 sons ( transposable 4x ) : 4b ( C333 / E333 / G#333 )
8) – ensemble de 6 sons ( transposable 6x ) : M5 : 5c ( CM5 / F#M5 )
9) – ensemble de 6 sons ( transposable 6x ) : 5f ( C2cb / F#2cb )
10) – ensemble de 6 sons ( transposable 6x ) : 5g ( C34d / F#34d )
11) – ensemble de 8 sons ( transposable 3x ) : M2 :3b ( CM2 / EbM2 / F#M2 / AM2 )
12) – ensemble de 8 sons ( transposable 6x ) : M4 : 5i ( CM4 / F#M4 )
13) – ensemble de 8 sons ( transposable 6x ) : M6 : 5j ( CM6 / F#M6 )
14) – ensemble de 9 sons ( transposable 4x ) : M3 : 4c ( CM3 / EM3 / G#M3 )
15) – ensemble de 10 sons ( transposable 6x ) : M7 : 5k ( CM7 / F#M7 )
( les références en italique renvoient au système de classification utilisé dans le programme MOLT explorer )
si on se limite aux 7 MOLT utilisés par OM, on dénombre 33 ‘transpositions’ et 22 modes marqués
les 33 transpositions :
1- CM1
2- C#M1
3- CM2
4- C#M2
5- DM2
6- CM3
7- C#M3
8- DM3
9- EbM3
10- CM4
11- C#M4
12- DM4
13- EbM4
14- EM4
15- FM4
16- CM5
17- C#M5
18- DM5
19- EbM5
20- EM5
21- FM5
22- CM6
23 – C#M6
24- DM6
25- EbM6
26- EM6
27- FM6
28- CM7
29- C#M7
30- DM7
31- EbM7
32- EM7
33- FM7
les 22 modes ‘marqués’:
pour chacun des 7 modes on prend en compte toutes les notes de départ possibles, qui génèrent des suites d’intervalles différentes / par exemple le mode majeur a 7 modes marqués ( cf série diationique: ionien, dorien, phrygien, lydien, mixolydien, aeolien, locrien )
C D E F G A B
D E F G A B C
E F G A B C D
F G A B C D E
G A B C D E F
A B C D E F G
B C D E F G A
vecteur intervallique similaire pour chaque mode, mais structure intervallique différente
M1 a 1 mode marqué / exemple pour CM1 :
C D E F# G# Bb
M2 a 2 modes marqués / exemple pour CM2 :
C C# D# E F# G A Bb ( CM2 )
C# D# E F# G A Bb C ( CM2 au départ de C# )
M3 a 3 modes marqués / exemple pour CM3 :
C D Eb E F# G G# A# B ( CM3 )
D Eb E F# G G# A# B C ( CM3 au départ de D )
Eb E F# G G# A# B C D ( CM3 au départ de Eb )
M4 a 4 modes marqués / exemple pour CM4 :
C C# D F F# G G# B ( CM4 )
C# D F F# G G# B C ( CM4 au départ de C# )
D F F# G G# B C C# ( CM4 au départ de D )
F F# G G# B C C# D ( CM4 au départ de F )
M5 a 3 modes marqués / exemple pour CM5 :
C C# F F# G B ( CM5 )
C# F F# G B C ( CM5 au départ de C# )
F F# G B C C# ( CM5 au départ de F )
M6 a 4 modes marqués / exemple pour CM6 :
C D E F F# G# A# B ( CM6 )
D E F F# G# A# B C ( CM6 au départ de D )
E F F# G# A# B C D ( CM6 au départ de E )
F F# G# A# B C D E ( CM6 au départ de F )
M7 a 5 modes marqués / exemple pour CM7 :
C C# D Eb F F# G G# A B ( CM7 )
C# D Eb F F# G G# A B C ( CM7 au départ de C# )
D Eb F F# G G# A B C C# ( CM7 au départ de D )
Eb F F# G G# A B C C# D ( CM7 au départ de Eb )
F F# G G# A B C C# D Eb ( CM7 au départ de F )
analyse chirurgicale des 7 modes
les modes symétriques (MATL) trouvent leur source dans la division de l’octave par 2 et par 3
la division de l’octave en 2 génère les modes M1, M2, M4, M5, M6 et M7
la division de l’octave en 3 génère les modes M1, M3
on peut généraliser la construction des 7 modes de manière linéaire, par ajouts d’intervalles symétriques autour des axes ( cf : SLONIMSKY ‘interpolation’ )
tous les exemples au départ de C :
M1 :
au départ de C-F#: interpolation de 2 notes
pour CM1 (= DM1=EM1=F#M1=G#M1=BbM1 ) : C +M2+M2 / F# +M2 +M2 : CDEF#G#Bb
au départ de C-E-G#: interpolation d’une note
pour CM1 (= DM1=EM1=F#M1=G#M1=BbM1 ) : C +M2 / E +M2 / G# +M2: CDEF#G#Bb
M2 :
au départ de C-F#: interpolation de 3 notes
pour CM2 : C +m2 +M2 +m2 / F# +m2 +M2 +m2 : CC#D#EF#GABb
pour DM2 : C +M2 +m2 +M2 / F# +M2 +m2 +M2 : CDEbFF#G#AB
M3 :
au départ de C-E-G#: interpolation de 2 notes
pour CM3 : C +M2 +m2 / E +M2 +m2 / G# +M2 +m2 : CDEbEF#GG#A#B
pour C#M3 : C +m2 +M2 / E +m2 +M2 / G# +m2 +M2 : CC#D#EFGG#AB
pour DM3 : C +m2 +m2 / E +m2 +m2 / G# +m2 +m2 : CC#DEFF#G#ABb
M4 :
au départ de C-F#: interpolation de 3 notes
pour CM4: C +m2 +m2 +m3 / F# +m2 +m2 +m3 : CC#DFF#GG#B
pour C#M4 : C +m2 +m2 +m2 / F# +m2 +m2 +m2 : CC#DD#F#GG#A
pour EM4 : C +m3 +m2 +m2 / F# +m3 +m2 +m2 : CD#EFF#ABbB
pour FM4 : C +m2 +m3 +m2 / F# +m2 +m3 +m2 : CC#EFF#GBbB
M5 :
au départ de C-F#: interpolation de 2 notes
pour CM5 : C +m2 + P4 / F# +m2 + P4 : CC#FF#GB
pour C#M5 : C +m2 +m2 / F# +m2 +m2 : CC#DF#GG#
pour FM5 : C +M3 +m2 / F# +M3 +m2 : CEFF#A#B
M6 :
au départ de C-F#: interpolation de trois notes
pour CM6: C +M2 +M2 +m2 / F# +M2 +M2 +m2 : CDEFF#G#A#B
pour DbM6 : C +m2 +M2 +M2 / F# +m2 +M2 +M2 : CDbEbFF#GAB
pour DM6 : C +m2 +m2 +M2 / F# +m2 +m2 +M2 : CC#DEF#GAbBb
pour EM6 : C +M2 +m2+m2 / F# +M2 +m2+m2 : CDD#EF#G#ABb
M7 :
au départ de C-F#: interpolation de quatre notes
pour CM7 : C +m2 +m2 +m2 +M2 / F# +m2 +m2 +m2 +M2 : CC#DEbFF#GG#AB
pour C#M7 : C +m2 +m2 +m2 +m2 / F# +m2 +m2 +m2 +m2 : CC#DEbEF#GG#Abb
pour EbM7 : C +M2 +m2 +m2 +m2 / F# +M2 +m2 +m2 +m2 : CDEbEFF#G#ABbB
pour EM7 : C +m2 +M2 +m2 +m2 / F# +m2 +M2 +m2 +m2 : CC#D#EFF#GABbB
pour FM7 : C +m2 +m2 +M2 +m2 / F# +m2 +m2 +M2 +m2 : CC#DEFF#GG#BbB
suivant cette logique d’inclusion, on notera que les modes 1, 2, 4, 5 et 6 sont tous présents dans le mode 7. De fait, il existe deux modes à transpositions limitées, le mode 3 et le mode 7, dans lesquels tous les autres sont contenus (voir tableaux)
mais comme le démontre la raison pour laquelle OM considère le mode 5 comme un mode à part entière (lire colors, M5 ), les 7 modes à transpositions limitées sont des ensembles de notes qui ont une couleur particulière / ainsi, l’architecture intervallique ‘réduite’ des modes 2, 4 et 6 ( inclus dans le mode 7 ) et du mode 1 ( inclus à la fois dans les modes 3, 6 et 7 ) leur donne une légitimité, la troncation aiguise les couleurs et génère des harmonies/mélodies singulières et angulaires.
à noter que les modes 5 et 7 disparaissent de l’analyse des modes à transpositions limitées dans le tome 7 du TRCO, ‘ à cause de leur parenté avec les autres modes – sans avoir pour autant renoncé aux harmonies qu’ils donnaient / le mode 5 était le même que le mode 4, moins 2 notes. Le mode 7 a été supprimé : ses harmonies n’ont donné lieu qu’à de rares passages, notamment dans les “CHANTS DE TERRE ET DE CIEL”, n°III, mesures 55 et 58 (…) ( YVONNE LORIOD in TRCO, tome 7, page 107 )
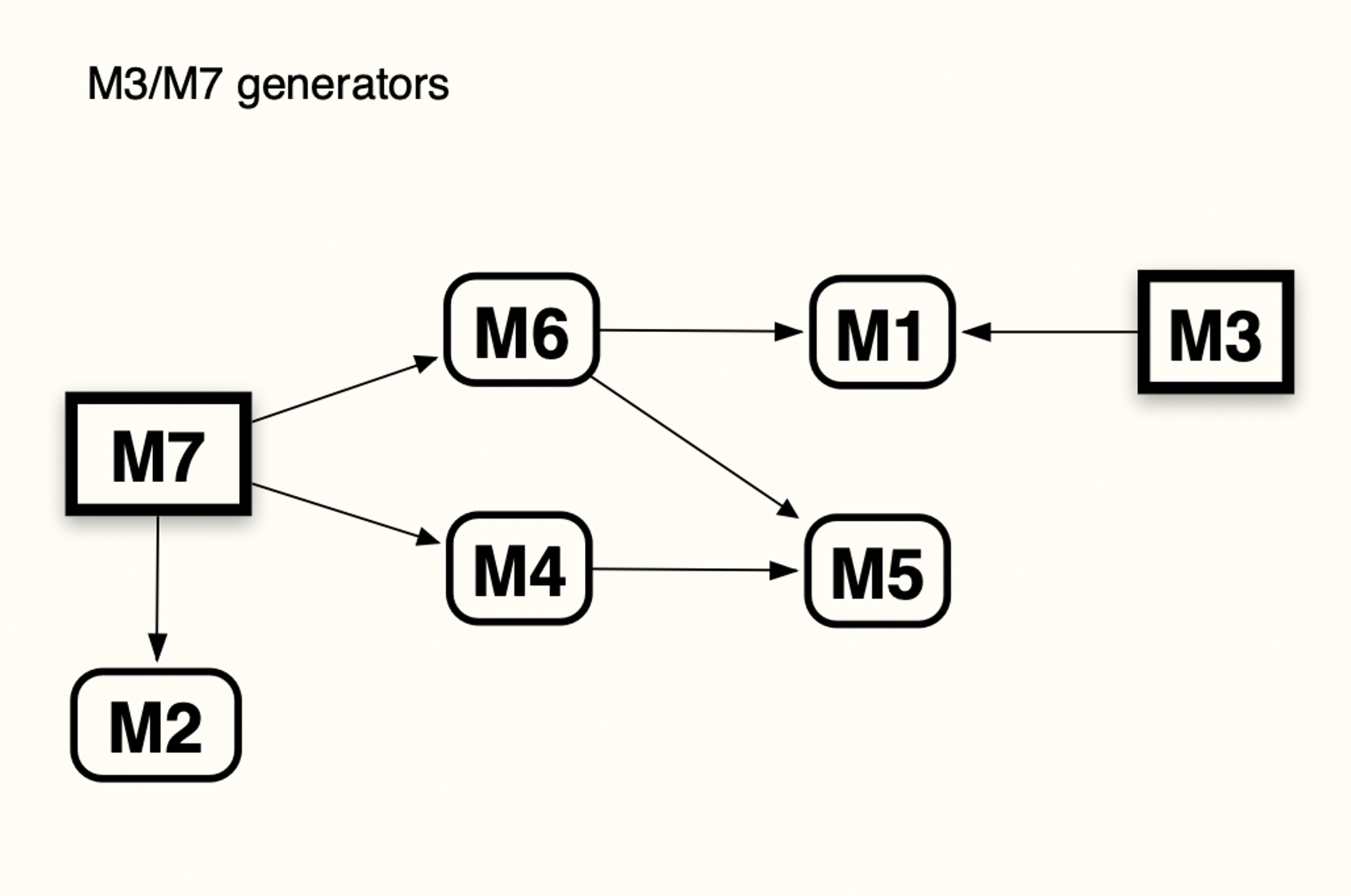
au départ de CM3 :
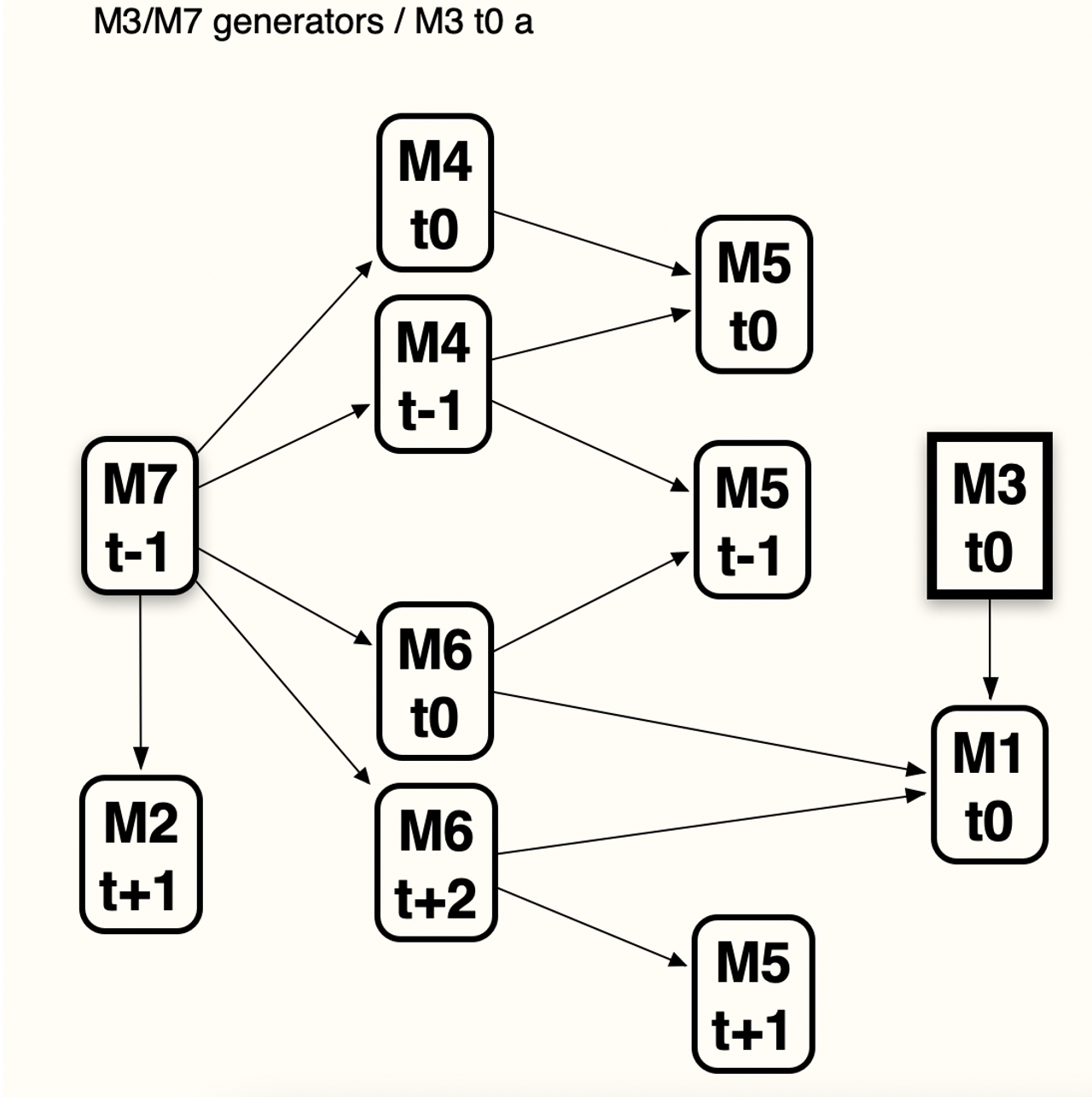
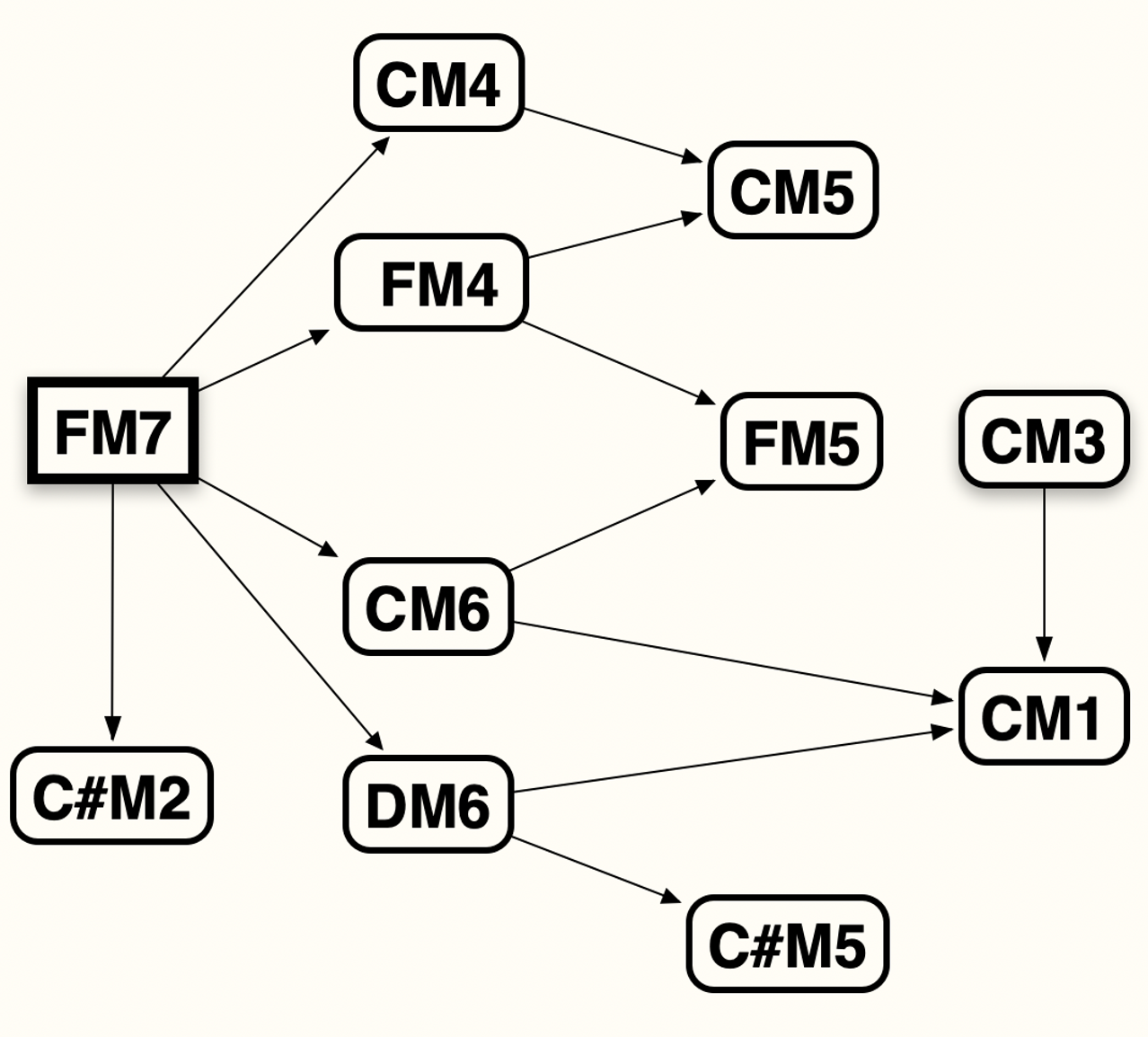
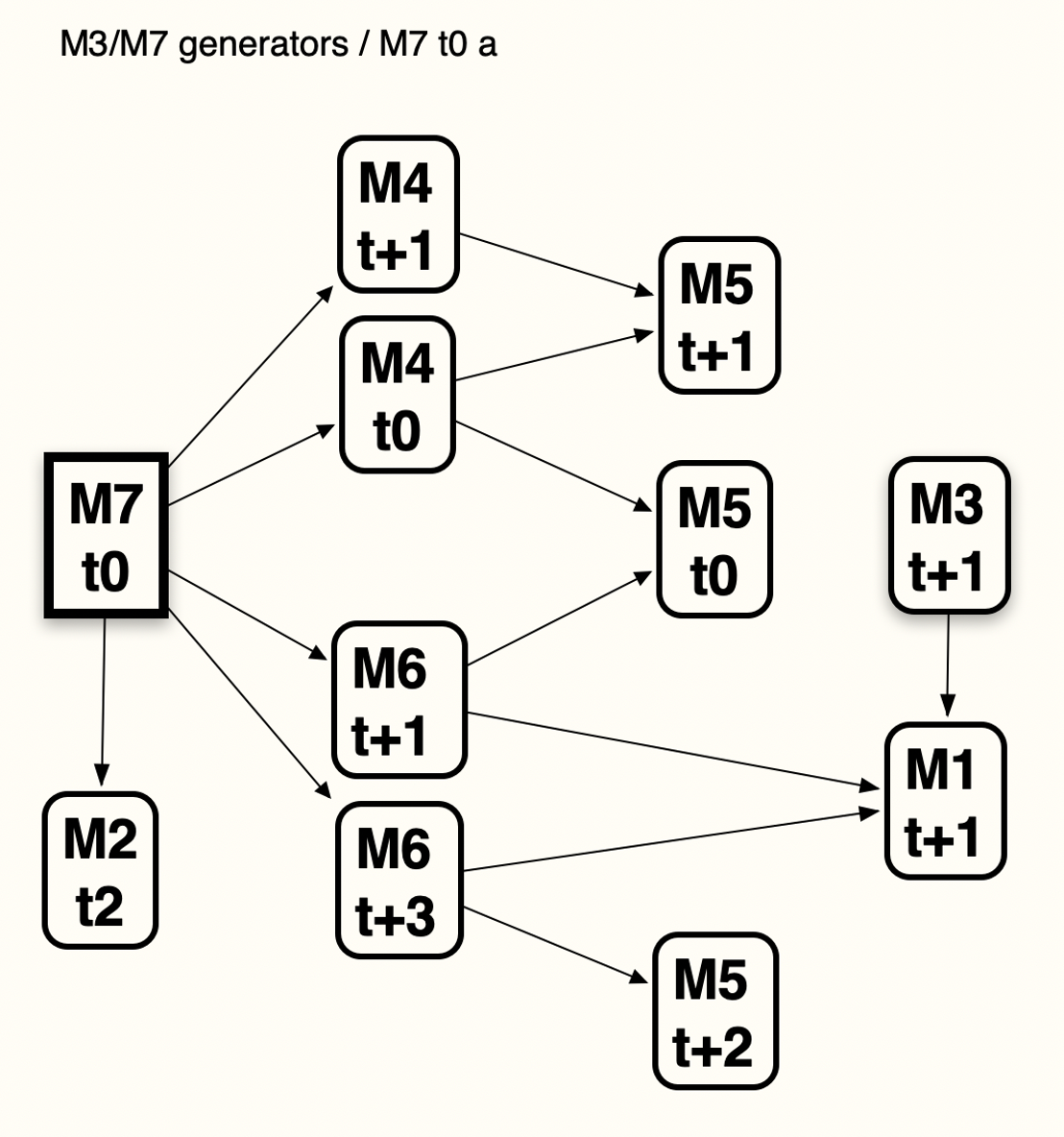
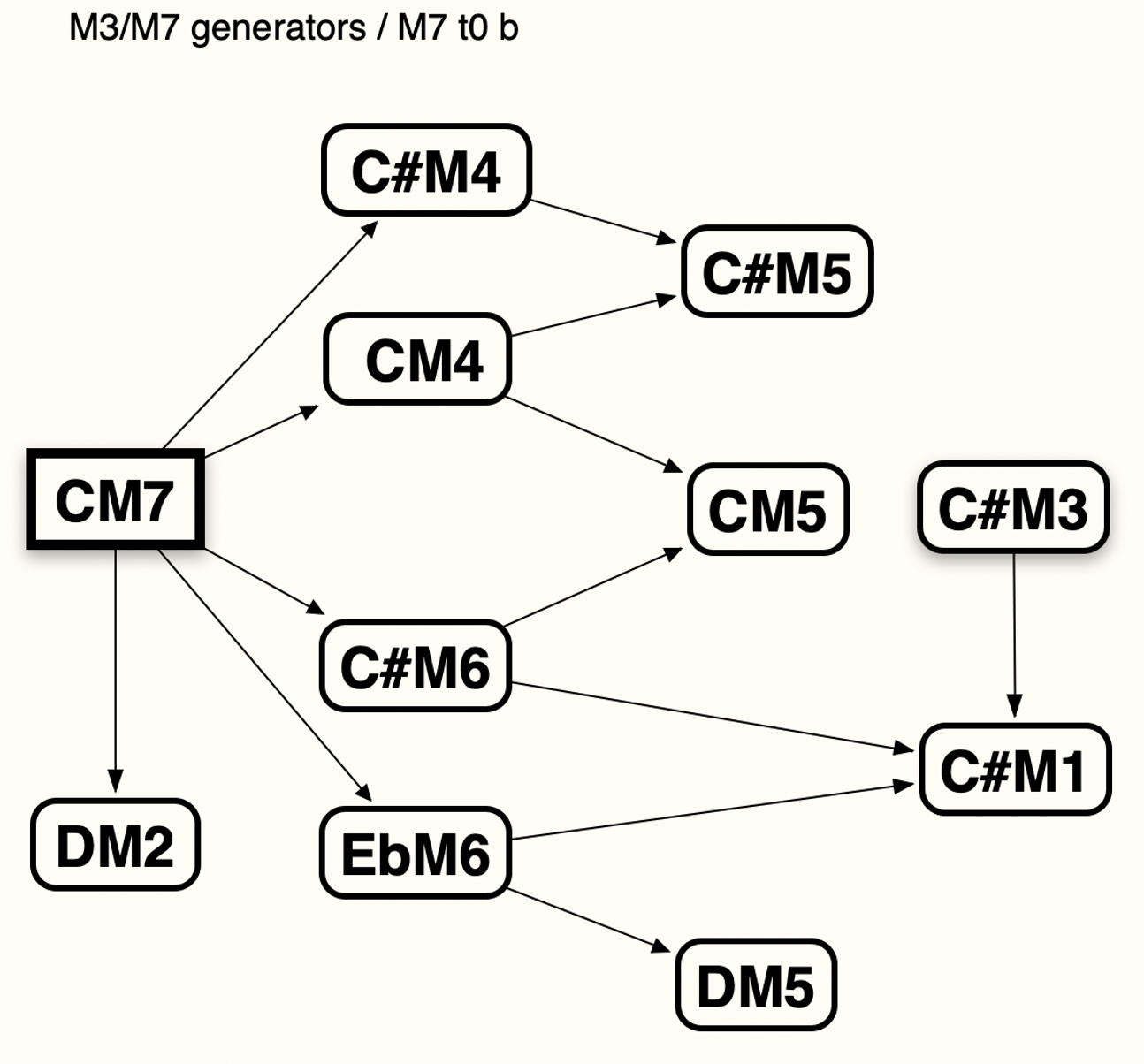
au départ de CM7 :
critères subjectifs
OM ne considère pas les ensembles 5a, 5b, 5d(=3a), 5e, 5f et 5g comme des modes à transpositions limitées, car ils sont soit des arpèges d’accords classés, soit des modes tronqués / idem pour les exemples 4a et 4b, qui sont des troncations du troisième mode.
ainsi, pour lui, un mode à transpositions limitées doit contenir minimum 8 notes ( excepté le mode 1 et le mode 5 ), et tous les autres ensembles symétriques issus de la division de l’octave en deux, trois ou quatre parties égales contenant moins de 6 notes ( ou 6 notes comme les ensembles 5f et 5g ) sont considérés comme des sous-ensembles ( ou troncations ) des modes à transpositions limitées:
5a est sous-ensemble de M1, M2, M3, M4, M5, M6 et M7
ex: C-F# est sous-ensemble CM1, CM2, DM2, CM3, DM3, CM4, C#M4, EM4, FM4, CM5, C#M5, FM5, CM6, DbM6, DM6, EM6, CM7, C#M7, EbM7, EM7 et FM7
5b est sous-ensemble de M2, M4, M5, M6 et M7
ex: B-C-F-F# est sous-ensemble de DM2, CM4, EM4, FM4, CM5, FM5, CM6, C#M6, CM7, EbM7, EM7,FM7
5d ( ou 3a ) est sous-ensemble de M2, M4, M6 et M7
ex: C Eb F# A est sous-ensemble de CM2, DM2, C#M4, EM4, C#M6, EM6, CM7, C#M7, EbM7, EM7
5f est sous-ensemble de M2, M4, M6 et M7
ex: C D F F# G# B est sous-ensemble de DM2, CM4, CM6, CM7, EbM7, FM7
5g est sous-ensemble de M2, M4, M6 et M7
ex: C Eb F F# A B est sous-ensemble de DM2, EM4, C#M6, CM7, EbM7, EM7
l’ordre de présentation est très probablement basé sur le nombre de transpositions de chaque mode :
mode 1 : 2 transpositions
mode 2 : 3 transpositions
mode 3 : 4 transpositions
mode 4, mode 5, mode 6, mode 7 : 6 transpositions*
*MESSIAEN did not say whether the numbering of modes 4 to 7, all transposable six times, rested on any particular criteria or was just arbitrarily decided (MESSIAEN’s triadic colouration: Modes as Interversion Author(s): CHEONG WAI-LING / source: music analysis , Mar., 2002, Vol. 21, No. 1, OLIVIER MESSIAEN (1908-92) anniversary issue (Mar., 2002), pp. 53-84
MATL / harmoniques + et –
les MATL pourraient également être lus comme résultantes de conjonction des harmoniques positives et négatives
un échange avec le saxophoniste STEVE COLEMAN sur le mode 3, qui peut être analysé comme la conjonction de toutes les partielles positives d’un son ( pour CM3, exemple au départ de C : C D E F# G G# A# B, manque Eb ), m’a aiguillé sur une autre lecture possible des 2 ‘modes-mères’, M3 et M7 / à titre informatif, ici quelques extraits de l’échange:
SC : for example MESSIAEN calls this nine tone structure a ‘chord of resonance’
D
B
Ab
F#
Eb
C
Bb
G
E
however, even though MESSIAEN does not actually say this, if we look closely at this you will see that it is really a 12-tone equal temperament version of the first fifteen partials of the positive harmonic series (overtone series) beginning on C and ascending (i.e. C G E Bb D F# Ab B) combined with the first fifteen partials of the negative harmonic series (undertone series) beginning on D and descending (i.e. D G Bb E C Ab F# Eb). So I am sure you can see the symmetry here. In the MESSIAEN book called « THE TECHNIQUE OF MY MUSICAL LANGUAGE » (Vol 1 = theory book and Vol 2 = example book) he lists the chords of superior and inferior resonance as follows, in which form he just calls the ‘chord of resonance”…
D -1
15 B Bb -5
13 Ab G -3
11 F# E -7
9 D C -9
7 Bb Ab -11
3 G Gb -13
5 E Eb -15
1 C
the numbers above are just the partial numbers – there are positive and negative partials because I am looking at this as the overtone and undertone series. As you can see when you use the superior and inferior chords in this relationship then you have the positive one as Cmaj and the negative one as negative Dmaj (which is really Gmin in normal language as ‘G’ is the root of negative Dmaj). Just think of it as an overtone series generated upwards from ‘C’ and an undertone series generated downward from ‘D’. Of course I did not duplicate any partials so partials 1, 3, 5, 7, 9, 11, 13 and 15 are C G E Bb D F# Ab B and partials -1, -3, -5, -7, -9, -11, -13 and -15 are D G Bb E C Ab F# Eb. Also all except the +-15th partials are duplicated in the other chord.
1 = -9
3 = -3
5 = -7
7 = -5
9 = -1
11 = -13
13 = -11
15 (not equal to) -15
So this is really a large symmetrical structure.
BV : regarding the example of symmetry you gave in the last mail, the ‘chord of resonance’ being the conjunction of the C Maj ascending partials and D Maj descending partials: from a theoretical point of view the conjunction of both overtone ( C ) and undertone ( D ) series gives the 3rd of the modes of limited transpositions ( in its 1st transposition : mode 3 of C : C D Eb E F# G G# A# B ) / and actually in each sum of the partials ( C or D ), there is only one note missing to obtain the entire mode 3 : in the sum of the C overtone series it is Eb that is ‘missing’ and in the sum of the D undertone series it is F#. It probably means that the other modes of limited transpositions could also be seen as the conjunctions of partials.
SC : I would be very interested to know. I noticed as soon as I looked as MESSIAEN’s modes that he was really dealing with the tempered overtone and undertone series in his own way. There is a great tradition going all the way back to the Egyptians and Babylonians of this idea, called by very different names in different eras. I just call it Musical Reciprocity.
BV : here the correlations between the modes of limited transpositions and the overtone and undertone series
( + ) = tempered overtone series / +C ( = -F# ) = C D E F# G G# A# B
( – ) = tempered undertone series / -C ( = +F# ) = C C# D E F F# Ab Bb
MN : missing notes
ON : ‘out’ notes
(all examples are related to C)
CM1 : is included in +C (-F#), +D (-Ab), +E (-Bb), +F# (-C), +G# (-D), +Bb (-E)
CM2 : is not entirely included in any overtone/undertone series
the ‘closest’ series are:
+F (-B) : MN: F#-A# / ON: F-B
+Ab (-D) : MN : A-C# / ON : Ab-D
+B (-F) : MN : C-E / ON : B-F
+D (-Ab) : MN : Eb-G / ON: D-G#
if we take +F as the reference, the conjunction with the following series is necessary to have all the 8 notes of CM2, but there will be 2 more ‘out notes’ ( the ON will be D-F-G#-B, which form the dimished triad that’s not in the CM2…) and actually will result in a 12 tone series. So there is no conjunction of series which gives as a resulting group of notes an entire and unique M2 without ‘out notes’
+F (-B) add +F# (-C) =CM2 ( ON: D-F-G#-B )
+F (-B) add +Ab (-D) =CM2 ( ON: D-F-G#-B )
+F (-B) add +Bb (-E) =CM2 ( ON : D-F-G#-B )
+F (-B) add +C (-F#) =CM2 ( ON : D-F-G#-B )
+F (-B) add +D (-Ab) =CM2 ( ON : D-F-G#-B )
+F (-B) add +E (-Bb) =CM2 ( ON : D-F-G#-B )
CM3 : is not entirely included in any overtone/undertone series
nb : as in M6, one note missing for the ‘closest’ series
the ‘closest’ series are:
+C (-F#) : MN :Eb
+E (-Bb) : MN : G
+Ab (-D) : MN : B
+C: the conjunction with the following series is necessary to have all the 9 notes of CM3 :
+C (-F#) add +E (-Bb) = CM3
+C (-F#) add +Ab (-D) = CM3
( +E (-Bb) add +Ab (-D) = CM3 )
So CM3 is the conjunction of +C and +E / +C and +Ab / +E and +Ab
CM4 : is not entirely included in any overtone/undertone series
+C (-F#) : MN : C#-F / ON : E-Bb
+C# (-G) : MN : D-F# / ON : Eb-A
+D (-Ab) : MN : F-G-B / ON : E-A-Bb
+Eb (-A) : MN : C-F#-G# / ON : Eb-A-Bb
+E (-Bb) : MN : C#-F-G / ON : Eb-E-Bb
+F (-B) : MN : D-F#-G# / ON : Eb-E-A
+F# (-C) : MN : G-B / ON : E-Bb
+G (-C#) : MN : C-Ab / ON : Eb-A
+Ab (-D) : MN : C#-F-B / ON : Eb-E-Bb
+A (-Eb) : MN : C-D-F# / ON : Eb-E-A
+Bb (-E) : MN : C#-G-B / ON : E-A-Bb
+B (-F) : MN : C-D-G# / ON : Eb-A-Bb
here, any overtone series combined with its tritone equivalent ( or with its parallel undertone series ) gives the entire M4 ( without adding more ‘out notes’ )
so with +C as reference :
+C (-F#) add +F#(-C) : you’ll get C C# D F F# G G# B (+2 out notes: E-Bb= FM7)
CM6 : is not entirely included in any overtone/undertone series
nb : as in M3, one note missing for the ‘closest’ series
the closest series are:
+C (-F#) : MN : F / ON : G
+E (-Bb) : MN : F / ON : D#
+F# (-C) : MN : B / ON : C#
+Bb (-E) : MN : B / ON : A
+C as reference:
+C (-F#) add +E (-Bb) =CM6 with 2 ON : Eb and G
+C (-F#) add +F# (-C) = CM6 with 2 ON : C# and G
+C (-F#) add +Bb (-E) = CM6 with 2 ON : G and A
CM7 : is not entirely included in any overtone/undertone series ( can’t be anyway, because it contains 10 notes ). But the conjunction of +C (-F#) and +F# (-C) gives FM7 without any ‘out notes’. / so C Mode 7 is the conjunction of positive C# and positive G
+C (-F#) add +F# (-C) = BM7
conclusion:
M3 and M7 could be seen as conjunctions of overtone/undertone series
( the only mode included in a single overtone or undertone series is M1 )